O Tangram tem, por um lado, uma componente lúdica, mas pode ser estudado de um ponto de vista matemático, sendo ainda uma importante ferramenta didática.
A antiga lenda chinesa do Tangram narra a história de um velho sábio deveria levar uma preciosa lâmina de vidro ao rei que precisava de uma janela em seu palácio.
O pedaço de vidro quadrado foi embrulhado em seda e lona e carregado na mochila do sábio.
A viagem foi longa, o sábio cruzou um deserto e rios, ele viajou por florestas e campos, até que chegou a uma cordilheira acidentada e escalou o cume de um pico alto e rochoso.
No topo da montanha, ele olhou ao longe e vislumbrou o palácio para o qual estava viajando.
Satisfeito por quase ter chegado, ele tropeçou e caiu pela encosta da montanha, quebrando o vidro.
Quando conheceu o rei, o sábio contou sobre sua viagem e admitiu que o vidro estava quebrado.
O vidro quadrado foi desembrulhado de sua caixa de seda e lona e o sábio ficou surpreso ao ver que o vidro não estava quebrado, mas dividido em sete formas geométricas.
O sábio moveu as formas e fez imagens para descrever sua jornada.
Ele mostrou ao rei sua casa, um camelo que vira no deserto, monges que encontrou no caminho, um barco no rio que cruzou e a cordilheira onde caiu.
O rei gostou das imagens geométricas e mandou recriar as formas em madeira.
Assim, segundo a lenda, os Tangrams foram inventados.
A HISTÓRIA OFICIAL DO TANGRAN
O quebra-cabeça Tangram pode ter até mais de 4000 anos de idade, dependendo de qual fonte você consultar: várias correntes de pesquisa debatem-se até hoje nesta controvérsia.
Até mesmo a origem do nome “Tangram” não é muito clara, mas todas as correntes concordam num ponto: a origem chinesa do Tangram.
Sam Lloyd (um especialista americano em quebra-cabeças) produziu uma versão adulterada para a origem do Tangram na qual declarava que o quebra-cabeças tinha sido criado há 4000 anos atrás pelo deus Tan.
Uma outra versão diz que um chinês chamado Tan deixou cair uma tábua quadrada de argila, a qual teria se partido em sete pedaços.
Enquanto tentava juntá-los para formar novamente o quadrado, teria composto várias outras formas.
Na China este quebra-cabeças era designado por Chi Pae Pan, que se pode traduzir por O Jogo das Peças da Sabedoria, ou ainda O Jogo das Sete Peças da Astúcia, e cada peça chama-se um tan.
As referências que existem sobre este jogo não são muito antigas se comparadas aos 4000 anos aludidos em algumas fontes.
De fato, conhece-se um embutido de 1780 onde se apresentam duas cortesãs a jogar o Tangram, e o primeiro livro chinês sobre o Tangram data de 1813, sendo provável a existência de edições anteriores.
A primeira publicação na Europa dá-se na Alemanha em 1805.
Independentemente de qual versão para a origem do Tangram é a verdadeira, desde há muito tempo centenas e centenas de formas têm sido registradas em vários livros.
O desafio do quebra-cabeças é recompor estas formas mudando as sete peças de posição.
O quebra-cabeça Tangram e muitos outros quebra-cabeças bidimensionais similares tornaram-se bastante populares no final do século XVIII e no início do século XX.
A CONSTRUÇÃO DO TANGRAN
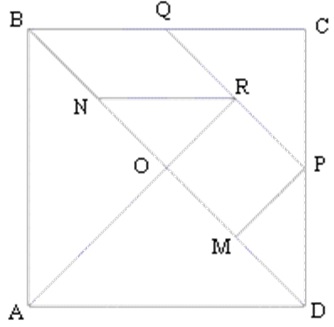
1) A partir de um quadrado ABCD, traça-se a sua diagonal DB, marca-se o seu ponto médio O e traça-se uma perpendicular a DB em O passando por A.
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
2) Marca-se os pontos médios, M de DO e N de OB.
3) Marca-se os pontos médios, P de DC e Q de CB. Traça-se o segmento PQ e marca-se o seu ponto médio R.
4) Traça-se os segmentos PM, OR e RN.
CONSTRUÇÕES COM O TANGRAN
É possível obter com o Tangram figuras que são aparentemente paradoxais, isto é, figuras em que parece que falta uma peça.
Há muitas figuras de grande elegância que podem ser construídas com o Tangram.
Abaixo vemos algumas delas.

Leia Mais:
- Jogos Matemáticos | 6 Jogos Clássicos Envolvendo Matemática.
- Problemas do Milênio | Os 7 Problemas de Matemática para o Século XXI
- Desafios de Matemática: Alguns problemas para desafiar sua mente!
- TEORIA DOS JOGOS | Matemática Aplicada à Sociologia e Economia
- O Princípio das Gavetas de Dirichlet e o Jogo do SIM | Teoria dos Jogos
- O Teorema de Bouton e a Solução do Jogo do NIM | Teoria dos Jogos

