A Sequência de Fibonacci: A Matemática por Trás da Natureza

Neste emocionante mergulho matemático, desvendaremos os mistérios por trás da famosa Sequência de Fibonacci e sua incrível presença em lugares inesperados. Imagine um mundo onde os números contam histórias fascinantes e seguem padrões surpreendentes. Neste artigo, exploraremos as origens dessa sequência, suas propriedades únicas e como ela se manifesta na natureza, na matemática, na arte e até mesmo na arquitetura.

Muitas pessoas foram apresentadas pela primeira vez aos números de Fibonacci por meio do best-seller de Dan Brown, “O Código Da Vinci”. No entanto, esses números têm uma história matemática rica e complexa que vai muito além da ficção.

Eles são creditados a um matemático italiano do século XIII, Leonardo Fibonacci, que desempenhou um papel fundamental na introdução dos numerais indo-arábicos na Europa, revolucionando a forma como fazemos cálculos.

Inspirados pelo livro “Almanaque das Curiosidades Matemáticas” de Ian Stewart, embarcaremos em uma jornada para explorar a vida e as contribuições de Fibonacci, revelaremos como sua famosa sequência surgiu a partir de um problema relacionado ao crescimento de coelhos e mergulharemos fundo em suas aplicações na matemática, na natureza, na arte e até na arquitetura.

Prepare-se para uma jornada fascinante pelo mundo dos números e suas conexões surpreendentes.

Quem foi Fibonacci?

Tudo começou em 1202, quando Leonardo de Pisa publicou o Liber abbaci, ou “Livro dos cálculos”, um texto sobre aritmética centrado principalmente em computações financeiras que promoveu o uso de numerais indo-arábicos, os precursores do sistema atual, que utiliza apenas 10 algarismos, de 0 a 9, para representar todos os números possíveis.

Leonardo Fibonacci, também conhecido como Leonardo de Pisa, foi um matemático italiano do século XIII. Ele nasceu por volta de 1170 e morreu cerca de 1240. Fibonacci é mais conhecido por introduzir na Europa o sistema numérico indo-arábico, que agora é universalmente usado em todo o mundo.

Fibonacci desempenhou um papel significativo na introdução dos números indo-arábicos (1, 2, 3, …, 9) e o conceito do zero ao mundo ocidental. Antes disso, a Europa usava principalmente o sistema de numeração romano, que era menos eficiente para cálculos matemáticos complexos.

Sua obra mais famosa é “Liber Abaci” (O Livro do Cálculo), publicada em 1202. Nesse livro, Fibonacci introduziu ao mundo ocidental a sequência de números que agora leva seu nome, a Sequência de Fibonacci. A sequência começa com 0 e 1, e cada número subsequente é a soma dos dois anteriores (0, 1, 1, 2, 3, 5, 8, 13, …).

A Sequência de Fibonacci, embora tenha sido introduzida por Fibonacci como parte de um problema sobre o crescimento de uma população de coelhos, tornou-se uma das sequências mais estudadas e reconhecidas na matemática, encontrando aplicações em diversos campos, desde a teoria dos números até a biologia e a arte.

Origens da Sequência de Fibonacci

Vamos começar nossa jornada explorando a história fascinante por trás da descoberta da Sequência de Fibonacci. Originária do trabalho do matemático italiano Leonardo Fibonacci no século XIII, essa sequência de números intrigou mentes curiosas por séculos.

Um dos exercícios do “Livro dos cálculos” parece ter sido uma invenção do próprio Leonardo. É o seguinte: “Um homem pôs um par de coelhos em um lugar cercado por paredes por todos os lados. Quantos pares de coelhos serão produzidos por esse par em um ano, se supusermos que a cada mês, cada par produzirá um novo par, que se tornará fértil a partir do 2º mês de vida?”

No começo, no mês 0, teremos 1 maduro.

No mês 1, esse par gera um par imaturo, portanto, temos 1 par maduro e 1 imaturo no total, 2 pares.

No mês 2, o par maduro gera outro par imaturo; o par imaturo amadurece, mas não gera nada. Então, agora temos 2 pares maduros e 1 par imaturo – no total, 3 pares.

No mês 3, os 2 pares maduros geram outros 2 pares imaturos; o par imaturo amadurece, mas sem gerar nada. Agora temos 3 pares maduros e 2 imaturos – 5 no total.

No mês 4, os 3 pares maduros geram outros 3 pares imaturos; os 2 pares imaturos amadurecem, mas não geram nada. E agora temos 5 pares maduros e 3 imaturos – 8 no total.

Continuando passo a passo, obtemos, para os meses 0, 1, 2, 3, …, 12, a sequência: $$ 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377$$

Como vemos, cada termo após o segundo é igual à soma dos dois termos anteriores. E assim, a resposta à pergunta de Leonardo é 377.

Algum tempo depois, provavelmente no século XVIII, Leonardo recebeu o apelido de Fibonacci “filho de Bonaccio”. O nome soava melhor que Leonardo Pisano Bigollo, que ele utilizava na época; assim, hoje em dia ele é conhecido apenas como Leonardo Fibonacci, e sua sequência de números é chamada Sequência de Fibonacci. A convenção moderna habitual manda colocar os números 0 e 1 na frente, gerando 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, embora o 0 inicial seja às vezes omitido. O símbolo para o n-ésimo número de Fibonacci é F_n , começando em F_0 = 0 .

Os números de Fibonacci são bastante inúteis como modelos de crescimento de populações reais de coelhos, embora processos mais gerais do mesmo tipo, chamados modelos de Leslie, sejam usados na compreensão da dinâmica de populações animais e humanas.

Ainda assim, esses números são importantes em diversas áreas da matemática, e também surgem no mundo natural – embora com menos frequência do que costuma ser sugerido. Já foram feitas grandes alegações sobre sua ocorrência nas artes, especialmente na arquitetura e na pintura, mas há muito poucas demonstrações concretas desse fato, a não ser quando os números são usados intencionalmente – por exemplo, no sistema “modulor” do arquiteto franco-suíço Le Corbusier.

A Sequência de Fibonacci e a Razão Áurea

A Sequência de Fibonacci é mais do que uma simples lista de números. Descubra suas propriedades matemáticas únicas, como a relação entre números consecutivos se aproximando da “Proporção Áurea” e como ela aparece em diversas áreas da matemática

Os números de Fibonacci têm fortes conexões com o número áureo, que, como você se lembra, é $$ \frac{(1 + \sqrt{5})}{ 2} = 1.618034…$$ A razão entre números de Fibonacci sucessivos, como 8 e 5, 13 e 8, 21 e 13, e assim por diante, se torna cada vez mais próxima de \phi à medida que a contagem cresce.

Ou então, como diriam os matemáticos, $$ F_n + \frac{1}{F_n}$$, tende a \phi quando n tende ao infinito. Por exemplo, 377/233 = 1.618025… De fato, para números inteiros de um certo tamanho, as frações de Fibonacci são as melhores aproximações possíveis do número áureo. Há até mesmo uma fórmula para o n-ésimo número de Fibonacci em termos de \phi : $$F_n = \frac{ \phi^n – (1 -\phi^n) }{\sqrt{5}}$$. E isso implica que F_n é o inteiro mais próximo de \dfrac{\phi ^n}{\sqrt{5}} .

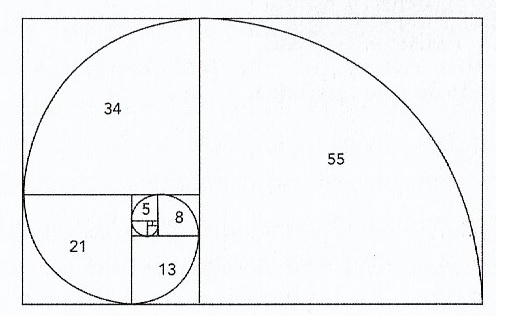
A Espiral de Fibonacci

Se formarmos quadrados cujos lados são números de Fibonacci, eles se encaixam muito ordenadamente, e poderemos desenhar quartos de círculos neles, criando a elegante espiral de Fibonacci. Como F_n é próximo de \phi ^n , essa espiral é muito próxima de uma espiral logarítmica, cujo tamanho cresce \phi a cada quarto de volta. Mas, como já disse, contrariando muitas afirmações, essa espiral não tem a mesma forma da espiral na concha do náutilo.

Manifestações da Sequência de Fibonacci na Natureza

Há uma ocorrência genuína e surpreendente – dos números de Fibonacci em criaturas vivas, particularmente nas plantas. As flores de uma quantidade impressionante de espécies têm pétalas em números de Fibonacci. Os lírios têm 3 pétalas, ervas-ciáticas têm 5, espori- nhas têm 8, calêndulas têm 13, ásteres têm 21, e a maioria das margaridas tem 34, 55 ou 89. Os girassóis muitas vezes têm 55, 89 ou 144.

Também há flores com outros números de pétalas, mas sua frequência é muito menor, e na maior parte desses casos vemos o dobro de um número de Fibonacci ou uma potência de 2. Às vezes, os números formam a Sequência de Lucas, relacionada à de Fibonacci: $$1, 3, 4, 7, 11, 18, 29, 47, 76, 123, …$$ Nela, novamente, cada número após o segundo é a soma dos dois anteriores, mas o início da sequência é diferente.

Parece haver boas razões biológicas para a ocorrência desses números. Podemos ver seus indícios mais fortes nos capítulos de margaridas e girassóis, quando as sementes já se formaram. Um capítulo é uma forma específica assumida pela florescência (a parte das plantas em que se localizam as flores), caracterizada pela alocação dessas flores em um receptáculo em forma de disco.

Neste caso, as sementes se dispõem em espirais:

Na margarida ilustrada, vê-se uma família de espirais que gira em sentido horário e outra a girar em sentido anti-horário. Há 21 espirais seguindo os ponteiros do relógio e 34 descrevendo trajetória contrária números de Fibonacci sucessivos. Padrões numéricos semelhantes, que também envolvem números de Fibonacci sucessivos, ocorrem em pinhas e abacaxis.

Os motivos precisos para o comportamento numérico de Fibonacci na vida vegetal ainda não estão completamente definidos, embora o tema já seja bastante bem compreendido. À medida que o broto da planta cresce, muito antes do surgimento das flores, algumas regiões do rebento formam pequenas protuberâncias, chamadas primórdios, das quais crescerão as sementes e outras partes essenciais da flor. Formam-se primórdios sucessivos em ângulos de 137,5° – ou 222,5° se subtrairmos esse valor de 360° fazendo a medição pelo outro lado. Isso é uma fração – 1 da circunferência completa de 360°.

Essa ocorrência da razão áurea pode ser prevista matematicamente se presumirmos que os primórdios se aglomeram da forma mais eficiente possível. Por sua vez, essa eficiência vem das propriedades elásticas do rebento que cres- ce – as forças que afetam os primórdios. A genética da planta também participa do processo.

Naturalmente, muitas plantas reais não seguem exatamente o padrão matemático ideal. Ainda assim, a matemática e a geometria associadas à Sequência de Fibonacci nos apresentam a noções importantes sobre essas características numéricas das plantas.

Conclusão

A Sequência de Fibonacci é muito mais do que uma sequência de números; é um fenômeno matemático rico em histórias e aplicações. Desde sua origem com Leonardo Fibonacci até suas manifestações na natureza, na arte e na arquitetura, essa sequência continua a encantar e inspirar todos aqueles que a exploram. Os números de Fibonacci são um lembrete de que a matemática e a natureza estão intrincadamente interligadas, criando um mundo de padrões e simetrias que nunca deixam de surpreender.

Leia Mais:

• Explorando o Fascinante Mundo dos Fractais: A Geometria da Natureza
• A beleza da matemática na Razão Áurea (ou Número de Ouro)
• Números Irracionais | Quais são, exemplos, história e as propriedades
• Modelo de Nagumo-Fitzhugh | A matemática aplicada à Neurociência