Neste post, exploraremos problemas matemáticos que se tornaram lendários por sua aparente simplicidade e a complexidade subjacente que os torna insolúveis. Desde a Quadratura do Círculo até o Problema das Pontes de Königsberg, cada um desses enigmas oferece uma visão fascinante sobre os limites da lógica e da razão.
Introdução
Imagine-se navegando por um vasto oceano de números e fórmulas, onde, de repente, surgem redemoinhos de mistérios aparentemente simples, mas que engolem qualquer tentativa de solução.
Ao longo da história, certos problemas matemáticos deixaram matemáticos e filósofos em longas travessias sem fim. Esses desafios não foram apenas obstáculos, mas verdadeiras bússolas que guiaram gerações na busca pelo conhecimento.
Neste artigo, vamos explorar os sete problemas sem solução que não apenas confundiram as mentes mais brilhantes, mas também abriram portas para descobertas revolucionárias.
Prepare-se para uma viagem através do tempo, onde cada enigma é um convite para entender os limites da razão humana e a vastidão da matemática.
Os 7 Problemas Sem Solução que Moldaram a História da Matemática
Ao longo dos séculos, problemas que pareciam simples em sua formulação revelaram-se extremamente complexos e, em muitos casos, impossíveis de resolver. Esses enigmas matemáticos, que vão desde a antiga Grécia até a era da computação, não apenas desafiaram o entendimento humano, mas também impulsionaram avanços fundamentais em diversas áreas do conhecimento.
A beleza desses problemas reside justamente nessa dualidade: a simplicidade de suas premissas versus a profundidade de suas consequências. Agora, vamos mergulhar de cabeça nos sete problemas que moldaram a história da matemática, revelando os mistérios e as lições que carregam.
Problema 1: A Quadratura do Círculo
A Quadratura do Círculo foi, por séculos, um dos problemas mais intrigantes da matemática. Formulado na Grécia Antiga, o desafio consistia em construir, com régua e compasso, um quadrado que tivesse exatamente a mesma área de um círculo. Simples à primeira vista, certo? Mas esse enigma, aparentemente inocente, desafiou as mentes mais brilhantes por quase dois milênios.
O objetivo era encontrar uma forma de transformar a área de um círculo (πr²) em um quadrado, sem recorrer a medições ou cálculos. Durante séculos, matemáticos como Arquimedes e Hipócrates de Quíos propuseram aproximações, tentando resolver o problema com ferramentas geométricas básicas. No entanto, as tentativas sempre esbarravam na mesma barreira: a natureza misteriosa de π.
A solução definitiva veio somente em 1882, quando o matemático alemão Ferdinand von Lindemann provou que π é um número transcendental. Isso significa que π não pode ser expresso como raiz de nenhuma equação polinomial com coeficientes racionais. Com isso, ficou provado que a quadratura do círculo com régua e compasso era impossível.
Essa descoberta foi mais do que o fim de um enigma clássico; foi um marco que revelou os limites da geometria clássica e impulsionou o estudo da teoria dos números. Além disso, a quadratura do círculo se tornou um símbolo para problemas que, apesar de parecerem simples, possuem uma complexidade que vai além do que o raciocínio humano pode resolver com as ferramentas convencionais.
Problema 2: A Duplicação do Cubo
A Duplicação do Cubo, também conhecida como o Problema de Delos, é outro enigma que desafiou matemáticos desde a Grécia Antiga. A lenda conta que, em tempos de praga, os oráculos instruíram os gregos a duplicar o volume do altar cúbico de Apolo para apaziguar os deuses. No entanto, o que parecia ser uma tarefa simples revelou-se um verdadeiro pesadelo geométrico.
O problema é simples na teoria: dado um cubo, como construir, usando apenas régua e compasso, outro cubo cujo volume seja exatamente o dobro do original? A questão pode ser traduzida matematicamente em encontrar uma maneira de construir uma aresta que seja a raiz cúbica de 2 vezes o comprimento da aresta original. No entanto, realizar isso com ferramentas geométricas básicas se provou impossível.
Ao longo da história, várias tentativas foram feitas. Matemáticos como Arquitas de Tarento e Eratóstenes propuseram soluções mecânicas engenhosas que, embora eficazes em termos práticos, não respeitavam a limitação das ferramentas puramente geométricas.
A prova definitiva da impossibilidade veio apenas em 1837, pelas mãos de Pierre Wantzel, um matemático francês. Ele demonstrou que a raiz cúbica de 2 não pode ser construída usando apenas régua e compasso, pois essa operação requer a resolução de uma equação cúbica. As ferramentas geométricas permitidas limitam-se a resolver equações polinomiais de até segundo grau, impossibilitando a construção de um cubo com o dobro do volume.
Essa descoberta não apenas encerrou a busca pela solução da duplicação do cubo, mas também lançou luz sobre os limites da construção geométrica, impulsionando o desenvolvimento da álgebra e da teoria das equações.
Problema 3: Trissecção do Ângulo
A Trissecção do Ângulo é mais um daqueles problemas que parecem simples, mas que desafiaram os matemáticos por milênios. O desafio era dividir qualquer ângulo dado em três partes iguais usando apenas régua e compasso. Pode até soar como uma tarefa trivial, mas a história mostrou que não era bem assim.
Desde a Grécia Antiga, matemáticos tentaram encontrar um método geral que funcionasse para qualquer ângulo. Arquimedes chegou a propor uma solução mecânica que envolvia a utilização de instrumentos adicionais, o que tecnicamente resolvia o problema, mas violava as regras estritas de usar apenas régua e compasso.
Foi somente em 1837, com o trabalho de Pierre Wantzel, que se provou ser impossível realizar a trissecção do ângulo com as ferramentas clássicas da geometria. A prova mostrou que, para a maioria dos ângulos, a trissecção exigia a solução de uma equação cúbica, o que está fora do alcance das construções com régua e compasso, que só resolvem equações de segundo grau.
Essa descoberta teve um impacto profundo no entendimento da geometria, ajudando a definir os limites do que era possível dentro das construções geométricas clássicas. Além disso, mostrou que, em muitos casos, a simplicidade de um problema pode esconder uma complexidade que só se revela através de ferramentas mais avançadas da matemática.
Problema 4: O Problema da Parada e a Computação Moderna
No início do século XX, com o surgimento da computação, a matemática começou a enfrentar novos tipos de problemas. Um dos mais importantes foi o Problema da Parada, formulado por Alan Turing em 1936. O desafio era simples de enunciar: será que existe um algoritmo capaz de determinar se qualquer programa de computador, dado qualquer entrada, terminará em algum momento ou continuará rodando indefinidamente?
Turing imaginou um cenário onde um computador (ou máquina) poderia ser programado para executar uma série de instruções. Mas ele logo percebeu que, para alguns programas, é impossível prever se eles irão parar ou entrar em um ciclo infinito. Para provar isso, Turing desenvolveu o conceito de uma “máquina de Turing”, um modelo teórico que simula a operação de um computador.
A grande sacada de Turing foi criar uma máquina que, ao tentar resolver o Problema da Parada, inevitavelmente se contradiz. Isso provou que não há um algoritmo universal que possa decidir, para todos os programas possíveis, se eles irão parar ou não. Em outras palavras, o Problema da Parada é indecidível.
Essa descoberta foi um marco para a ciência da computação, estabelecendo os limites do que pode ser computado. O trabalho de Turing não apenas definiu os fundamentos da teoria da computabilidade, mas também abriu portas para áreas como a criptografia e a inteligência artificial, impactando profundamente o desenvolvimento da tecnologia moderna.
Problema 5: Hipótese de Continuum e os Fundamentos da Matemática
Proposta por Georg Cantor no final do século XIX, a Hipótese do Continuum é um dos problemas mais profundos e fascinantes da matemática. Ela lida com a natureza dos infinitos e pergunta se existe um conjunto infinito que tenha mais elementos do que os números naturais, mas menos do que os números reais. Em termos simples: existe algum “infinito intermediário” entre o tamanho dos números inteiros e o dos números reais?
Cantor conjecturou que não, ou seja, não existe tal conjunto intermediário. Esse enigma, que pode parecer abstrato, toca diretamente os fundamentos da matemática e da lógica. Durante décadas, matemáticos tentaram provar ou refutar a hipótese. Kurt Gödel, em 1940, mostrou que a Hipótese do Continuum não pode ser refutada a partir dos axiomas da matemática estabelecidos (os axiomas de Zermelo-Fraenkel com o Axioma da Escolha). Mais tarde, em 1963, Paul Cohen provou que ela também não pode ser provada a partir desses axiomas.
Essa combinação de resultados significa que a Hipótese do Continuum é independente dos axiomas tradicionais da matemática. Em outras palavras, nossa compreensão atual dos fundamentos da matemática é insuficiente para resolver o problema, e tanto aceitar quanto rejeitar a hipótese pode ser considerado matematicamente válido.
Essa descoberta abalou a teoria dos conjuntos e a forma como entendemos o infinito. Ela revelou que algumas perguntas, por mais que desejemos uma resposta definitiva, podem simplesmente estar além do alcance dos axiomas tradicionais da matemática.
Problema 6: O Problema dos Três Corpos e a Mecânica Celeste
O Problema dos Três Corpos é um dos grandes desafios da mecânica celeste, formulado originalmente para descrever as interações gravitacionais entre três corpos no espaço, como o Sol, a Terra e a Lua. A questão parece simples: dado o estado inicial de três corpos de massas arbitrárias, como prever suas trajetórias sob a influência de sua gravidade mútua?
Isaac Newton foi o primeiro a explorar essa questão no século XVII, mas, ao contrário do caso de dois corpos (que ele resolveu com as leis do movimento), as equações que descrevem três corpos em interação são altamente complexas e não lineares. Pequenas variações nas condições iniciais podem levar a resultados extremamente diferentes, tornando o sistema essencialmente imprevisível.
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
O matemático francês Henri Poincaré, no final do século XIX, mostrou que não existe uma solução analítica geral para o Problema dos Três Corpos. Ele descobriu que esse sistema exibe um comportamento caótico, onde previsões de longo prazo se tornam praticamente impossíveis devido à sensibilidade às condições iniciais – o que hoje é conhecido como a “teoria do caos”.
Esse resultado não apenas revolucionou o estudo dos sistemas dinâmicos, mas também teve implicações muito além da mecânica celeste. A teoria do caos agora é aplicada em áreas tão diversas quanto a meteorologia, a biologia e a economia, mostrando como pequenos fatores podem ter grandes impactos em sistemas complexos.
 Sugestão de Leitura: Clique aqui e desvende o enigma cósmico em ‘O Problema dos Três Corpos’.
Sugestão de Leitura: Clique aqui e desvende o enigma cósmico em ‘O Problema dos Três Corpos’.
Problema 7: O Enigma das Pontes de Königsberg
No século XVIII, a cidade de Königsberg, na Prússia (atual Kaliningrado, na Rússia), era cortada pelo rio Pregel, com várias ilhas conectadas ao continente por sete pontes. O desafio era simples: seria possível caminhar pela cidade cruzando todas as pontes uma única vez, sem repetir nenhuma? Esse enigma intrigou tanto os habitantes locais quanto os matemáticos da época, mas ninguém conseguia encontrar uma solução.
Foi somente em 1736 que Leonhard Euler, um dos maiores matemáticos da história, resolveu o enigma de uma forma completamente inovadora. Ao invés de focar nas rotas específicas, ele abstraiu o problema, representando as massas de terra como vértices e as pontes como arestas que ligavam esses vértices. Assim, ele criou um grafo, o que lhe permitiu estudar a estrutura do problema em termos puramente matemáticos.
Euler provou que não havia como cruzar todas as pontes de Königsberg sem repeti-las, pois, para que tal caminho existisse, cada vértice (ou massa de terra) deveria ter um número par de pontes conectadas a ele. No caso de Königsberg, todas as massas de terra tinham um número ímpar de pontes, tornando o caminho impossível.
A solução de Euler não apenas resolveu o problema, mas também deu origem à teoria dos grafos, um ramo da matemática que hoje é fundamental na ciência da computação, logística e em diversas outras áreas. O Enigma das Pontes de Königsberg foi o primeiro passo para o desenvolvimento de uma nova forma de pensar sobre redes e conexões.
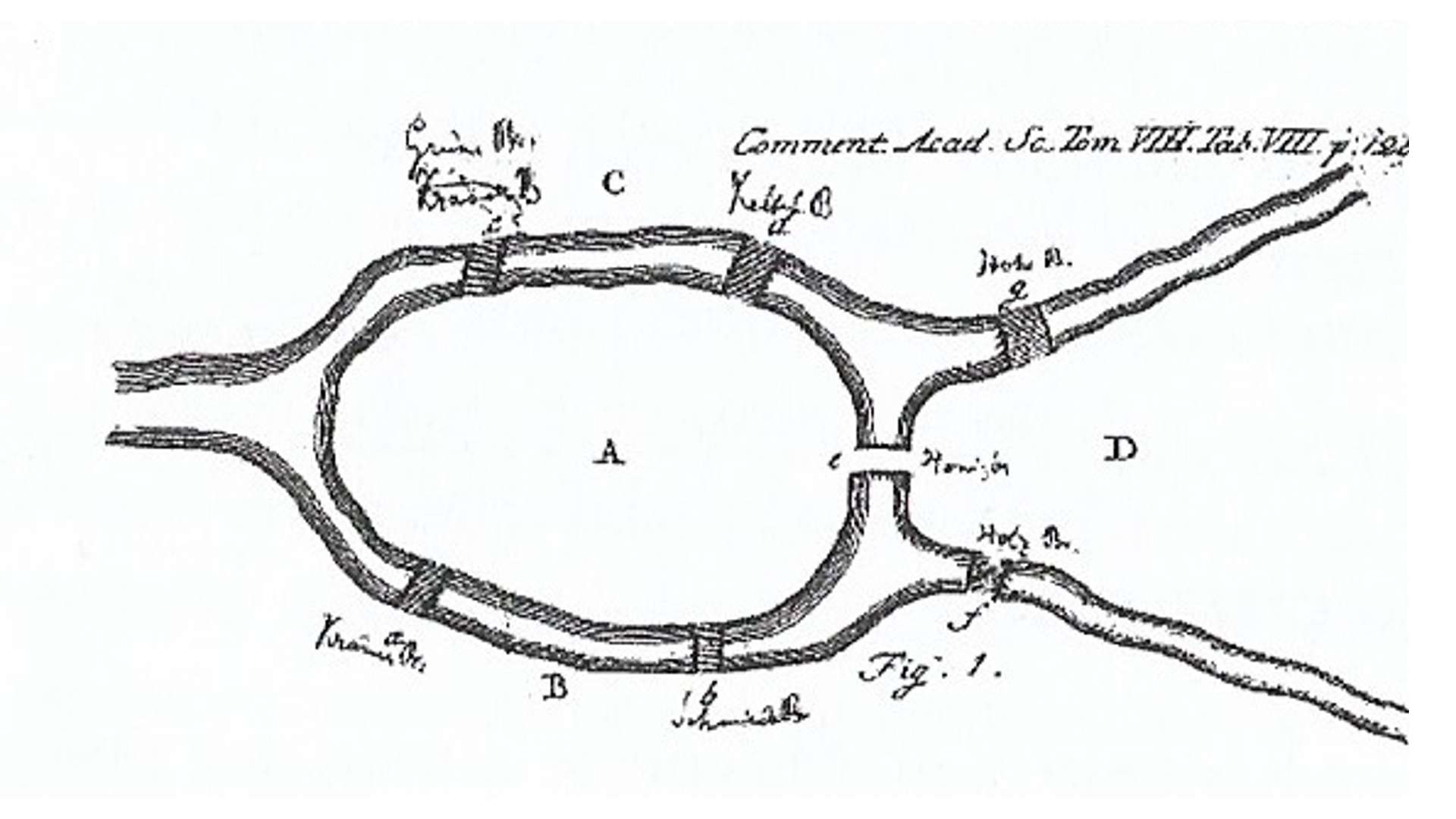 O desenho das pontes de Königsberg feito por Euler.
O desenho das pontes de Königsberg feito por Euler.
Conclusão
Ao longo deste artigo, exploramos alguns dos problemas mais intrigantes e desafiadores que a matemática já enfrentou. Desde a Quadratura do Círculo até o Problema dos Três Corpos, cada um desses enigmas não apenas testou os limites do conhecimento humano, mas também abriu caminho para novas áreas de estudo e compreensão.
A grande lição que esses problemas nos ensinam é que, muitas vezes, o verdadeiro valor está na jornada da descoberta, nas tentativas e nos fracassos que impulsionam o progresso. Mesmo sem uma solução definitiva, cada desafio ampliou os horizontes da matemática, provando que o desconhecido pode ser uma fonte poderosa de inspiração.

