Uma Introdução ao Laplaciano em Diferentes Sistemas de Coordenadas

O Laplaciano é um objeto matemático que surge frequentemente em equações diferenciais parciais oriundas de modelagens de fenômenos da ciência e da engenharia.

O Laplaciano de uma função escalar u(x,y,z), em coordenadas retangulares tridimensionais (x,y,z) , é um operador diferencial escalar definido por $$ \nabla ^2 u= \frac{\partial ^2 u}{\partial x^2} + \frac{\partial ^2 u}{\partial y^2} + \frac{\partial ^2 u}{\partial z^2} .$$

Assim, o Laplaciano de uma função escalar u(x,y,z) nada mais é do que o divergente do gradiente de u(x,y,z).

Obviamente, conforme o tipo do problema em estudo, a escolha do sistema adequada de coordenadas pode ser importante para a obtenção da solução. Por exemplo, em um cilindro, é conveniente usar coordenadas cilíndricas; enquanto se o problema envolve uma esfera, a escolha natural será coordenadas esféricas.

O Laplaciano é extremamente importante em mecânica, eletromagnetismo, teoria ondulatória e mecânica quântica, e aparece na equação de Laplace $$ \nabla ^2 \phi = 0,$$ na equação diferencial de Helmholtz $$ \nabla ^2 \phi + k^2 \phi = 0,$$ na equação da onda $$ \nabla ^2 \phi = \frac{1}{v^2} \frac{ \partial ^2 \phi }{ \partial t^2 },$$ e também na equação de Schrödinger

É interessante observar que um operador análogo é obtido pela generalização de três dimensões para o espaço-tempo quadridimensional é denotado por \Box ^2 e é conhecido como d’Alembertiano, ou operador de d’Alembert.

Uma versão do Laplaciano que opera em funções vetoriais é conhecida como vetor Laplaciano, e um tensor Laplaciano pode ser definido de forma semelhante. Um vetor Laplaciano também pode ser definido, assim como sua generalização para um tensor Laplaciano.

O quadrado do Laplaciano \left( \nabla ^2 \right)^2 = \nabla ^4 é conhecido como o operador biharmônico.

EXEMPLO (A Transformação de uma integral dupla do Laplaciano de uma função em uma integral de linha)

Seja w(x,y) uma função a qual é contínua e tem derivadas contínuas de primeira e segunda ordem em alguma região R do plano x0y da forma indicada no Teorema de Green.

Vamos assumir que $$ f = -\frac{\partial w}{\partial y} \qquad g = \frac{\partial  w}{\partial  x} $$ que são contínuas em R , e $$ \frac{\partial g}{\partial x} – \frac{\partial f}{\partial y} = \frac{\partial ^2 w}{\partial x^2}+ \frac{\partial ^2 w}{\partial y^2} = \nabla ^2 w,$$ o Laplaciano de w .

Desta forma, $$ \int{C}{(fdx+gdy)} = \int_{C}{\left( f \frac{dx}{ds} + g \frac{dy}{ds} \right) ds} = \int_{C}{\left( – \frac{\partial w}{\partial y} \frac{dx}{ds} + \frac{\partial w}{\partial x} \frac{dy}{ds} \right) ds}$$ onde s é o comprimento de arco de C que é uma curva orientada como mostrado na figura abaixo.

O integrando da última integral pode ser escrita como um produto escalar dos vetores $$ \nabla w = \frac{\partial w}{\partial  x} \vec{i} + \frac{\partial w}{\partial  y} \vec{j} \qquad e \qquad \vec{n} = \frac{dy}{ds} \vec{i} – \frac{dx}{ds} \vec{j};$$ ou seja, $$- \frac{\partial w}{\partial y} \frac{dx}{ds} + \frac{\partial w}{\partial x} \frac{dy}{ds} = \nabla w \cdot \vec{n}.$$

O vetor \vec{n} é um vetor normal a C , por causa do vetor $$ \vec{n} = \frac{d \vec{r} }{ds} = \frac{dx}{ds} \vec{i} + \frac{dy}{ds} \vec{j} $$ ser um vetor tangente unitário a C e \vec{n} \cdot \vec{u} = 0. Desta forma, podemos ver que \vec{n} é direcionada para o exterior de R .

Logo, podemos garantir que \nabla w \cdot \vec{n} é a derivada de w na direção da normal externa de C . Denotando esta derivada direcional por \dfrac{\partial w}{\partial \vec{n}} , obtemos, usando o Teorema de Green, que $$ \iint\limits_{R}{\nabla ^2 w dx dy } = \int_{C}{ \frac{\partial w}{\partial \vec{n}} ds .}$$

O Laplaciano em Coordenadas Cilíndricas

As coordenadas cilíndricas de um ponto P, cujas coordenadas cartesianas são (x,y,z), no espaço são dadas por $$r, \theta, z$$ onde r e \theta são as coordenadas polares da projeção de P sobre o plano xy .

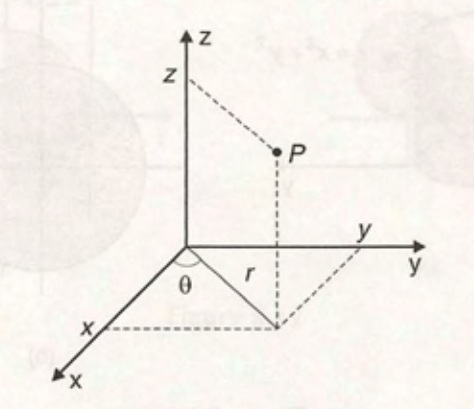
O Laplaciano em coordenadas cilíndricas (r , \theta , z) é dado por $$ \nabla ^2 u= \frac{\partial ^2 u}{\partial r^2} + \frac{1}{r} \frac{\partial u}{\partial r} + \frac{1}{r^2} \frac{\partial ^2 u}{\partial \theta ^2} + \frac{\partial ^2 u}{\partial z^2} $$ observando que r \geq 0, 0 \leq \theta < 2 \pi e - \infty < z < \infty .

O Laplaciano em Coordenadas Esféricas

As coordenadas esféricas de um ponto P, cujas coordenadas cartesianas são (x,y,z), no espaço são dadas por $$r, \theta, \phi$$ onde r é a distância de P até a origem, \theta é mesma das coordenas cilindricas e \phi é o ângulo formado pelo eixo positivo dos z e o segmento que une o ponto P à origem.

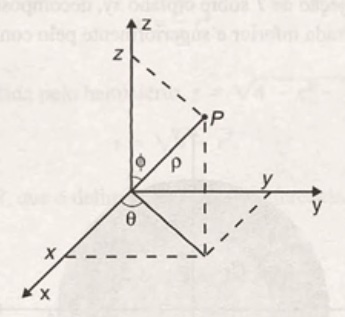
O Laplaciano em coordenadas cilíndricas (r , \theta , \phi) é dado por $$ \nabla ^2 u= \frac{1}{r^2} \frac{\partial }{\partial r} \left( r^2 \frac{\partial u}{\partial r} \right) + \frac{1}{r^2 sen \theta } \frac{\partial }{\partial \theta} \left( sen \theta \frac{\partial u}{\partial \theta} \right)+ \frac{1}{r^2 sen^2 \theta } \frac{\partial ^2 u}{\partial \phi ^2} $$ observando que r \geq 0, 0 \leq \theta < \pi e 0 \leq \phi < 2 \pi .

O Laplaciano em Coordenadas Parabólicas

Um sistema de coordenadas curvilíneas no qual dois conjuntos de superfícies de coordenadas são obtidos girando as parábolas de coordenadas cilíndricas parabólicas em torno do eixo x, que é então renomeado como eixo z.

As equações para as coordenadas parabólicas são $$ x = u v \text{cos} \theta $$ $$ y = u v \text{sen} \theta $$ $$ z = \frac{1}{2} \left( u^2 – v^2 \right)$$ onde $$ u \in [0, \infty ), \qquad v \in [0, \infty ) \qquad e \qquad \theta \in [0, 2 \pi ).$$

Nestas condições, o Laplaciano é dado por $$ \nabla ^2 f = \frac{1}{u^2 + v^2} \left( \frac{1}{u} \frac{\partial f}{\partial u} + \frac{\partial ^2 f}{\partial u^2} + \frac{1}{v} \frac{\partial f}{\partial v} + \frac{\partial ^2 f}{\partial v^2}\right) + \frac{1}{u^2 v^2} \frac{\partial ^2 f}{\partial \theta ^2}.$$

A equação diferencial de Helmholtz, por exemplo, será separável se escrita em coordenadas parabólicas.

O Laplaciano e o Conceito da Divergência

A divergência é um operador vetorial que opera em um campo vetorial. Este último pode ser pensado como representando um fluxo de um líquido ou gás, onde cada vetor no campo vetorial representa um vetor de velocidade do fluido em movimento.

Grosso modo, a divergência mede a tendência do fluido de se acumular ou se dispersar em um ponto e usando o operador nabla (ou del), \nabla , a divergência é denotada por \nabla \cdot e produz um valor escalar quando aplicado a um campo vetorial, medindo a quantidade de fluido em cada ponto.

Seja $$\vec{F}(x,y,z) = F_1(x,y,z) i + F_2(x,y,z)j + F_3(x,y,z)k$$ o campo vetorial definido em um aberto A do \mathbb{R}^3 e suponha que F_i admita derivadas parciais para i=1,2,3.

O divergente de \vec{F}, que se denota por div(\vec{F}), é o campo vetorial definido em A e dado por $$div\left( \vec{F} \right) = \frac{\partial F_1}{\partial x} + \frac{\partial F_2}{\partial y} + \frac{\partial F_3}{\partial z} = \nabla . \vec{F}$$ onde \nabla é o vetor gradiente.

Então, o Laplaciano (ou seja, a divergência do gradiente) de f pode ser definido pela soma das segundas derivadas parciais não misturadas: $$ \nabla \cdot \nabla f = \nabla ^2 f$$ e pode, de forma equivalente, ser considerada como o traço (tr) da matriz Hessiana da função f , que aquela que contém as segundas derivadas parciais próprias (ou não misturadas) na diagonal.

Ou seja, $$ \nabla ^2 f = \text{tr} \left( H(f) \right)$$ lembrando que o traço define a soma dos elementos na diagonal principal de uma matriz quadrada n \times n , que neste caso é a Matriz Hessiana, e também a soma de seus autovalores.

O Laplaciano e a Equação de Laplace

Uma das mais importantes equações diferenciais parciais que aparecem em fenômenos físicos é a equação de Laplace: $$ \nabla ^2 \phi = \frac{\partial ^2 u}{\partial x^2} + \frac{\partial ^2 u}{\partial y^2} + \frac{\partial ^2 u}{\partial z^2} = 0.$$ A teoria da solução da equação de Laplace é chamada de teoria potencial e as soluções desta equação que possuam derivadas parciais de segunda ordem contínuas são ditas funções harmônicas.

A Interpretação Física do Laplaciano

Através de um desenvolvimento em série de Taylor em torno de um ponto r_0 é possível demonstrar que o laplaciano nesse ponto é proporcional à diferença entre o valor médio \overline{ \phi } do campo no elemento de volume em torno do ponto e o valor \phi _0 do campo em r_0 . Este resultado permite-nos interpretar imediatamente as equações que contenham o operador laplaciano.

Um exemplo particularmente importante é o da equação de Laplace  vista anteriormente que governa o potencial eletrostático no vazio. Esta equação basicamente informa-nos então que o valor médio do potencial em torno de um ponto P é igual ao valor do potencial no próprio ponto P .

No eletromagnetismo, os campos eléctrico e magnético são comummente especificados pela respectiva divergência e rotacional, pelo que este resultado assume grande importância. Faremos dele uso abundante. A condição fronteira exigida é a especificação da componente normal do campo na fronteira da região. Se, conforme acontece nas situações típicas do eletromagnetismo, a região se estender até ao infinito, o campo vetorial é completamente especificado pela sua divergência e pelo seu rotacional, desde que tenda apropriadamente para zero no infinito; um resultado conhecido por teorema de Helmholtz.

Leia Mais Sobre Cálculo de Várias Variáveis:

• Diferenciabilidade de Funções de Várias Variáveis a Valores Reais
• Derivada Direcional de Funções de Várias Variáveis
• O Divergente de um Campo Vetorial | Definição e Interpretação
• Funções de Variáveis Complexas | Diferenciabilidade e Funções Analíticas
• Equações Diferenciais Parciais | Uma Introdução aos Conceitos Básicos

Referências Bibliográficas do Artigo:

1. Wilfred Kaplan – “Advanced Calculus” [Link do livro]
2.  Erwin Kreyszig – “Matemática Superior para Engenharia – Vol. 1 e 2” [Link do livro 1] [Link do livro 2]
3. Hamilton Luiz Guidorizzi – “Um Curso de Cálculo, vol. 3” [Link do Livro]