PRECISANDO DE AJUDA COM SEUS EXERCÍCIOS SOBRE ESTE CONTEÚDO? Entre em contato com a gente via WhatsApp clicando aqui. |
Nossa relação com o universo se baseia basicamente em medições. Até por isso, grandezas e medidas são essenciais para construir o pensamento científico. Entre as principais grandezas estão o comprimento, o tempo, a massa, a temperatura, a pressão e a resistência elétrica que vão além do estudo da física, por exemplo.
Classificação e Medida
O método mais simples de medida é o de classificar os objetos e eventos. Designamos os objetos por palavras, símbolos ou números. Este é o tipo mais primitivo de escala e denominado escala nominal, estando no nível nominal, onde não há indicação de classificação.
Neste momento existe a falta de informação quantitativa, mas uma clara definição de objetos já um princípio de medição e classificação científica. Obteremos uma escala mais útil se formos bem sucedidos na classificação de objetos e eventos. Se formos capazes de classificar os objetos e eventos estaremos trabalhando com uma escala ordinal, estando no nível ordinal, onde a classificação é possível e os intervalos não são definidos.
Quando as escalas possuem um significado científico, obteremos uma escala com intervalos significativos que chamamos de escala graduada, onde chegamos ao nível de intervalos, onde a classificação é possível, os intervalos são definidos, o ponto de referência é arbitrário, as proporções não tem significado.
Existem escalas que são até mais úteis do que as nominais, ordinais ou graduadas, como a escala de proporcionalidade, onde a classificação é possível, os intervalos são definidos, o ponto de referência é absoluto, as proporções e percentagens são significativas.
Esta importante distinção entre vários níveis de medida é devida a S. S. Stevens, no artigo de 1951, intitulado “Mathematics, measurement, and psychophysics”. À luz da escala multidimensional de Stevens, os dois primeiros níveis, Nominal e Ordinal, são frequentemente chamados de não–métricos . Os dois últimos são métricos.
O que é Sistema Internacional de Unidades?
Para descrever uma grandeza física, precisamos definir primeiramente uma unidade, que é uma medida da grandeza cujo valor é definido como exatamente 1,0. Em seguida, é necessário definir um padrão, que será uma referência com a qual devem ser comparados todos os outros exemplo da grandeza.
Todas as unidades e seus padrões são estabelecidos de forma que os cientistas concordem que essas definições são práticas e razoáveis. Para organizar o padrão das grandezas fundamentais, que devem ser acessíveis e invariáveis, foi estabelecido o Sistema Internacional de Unidades.
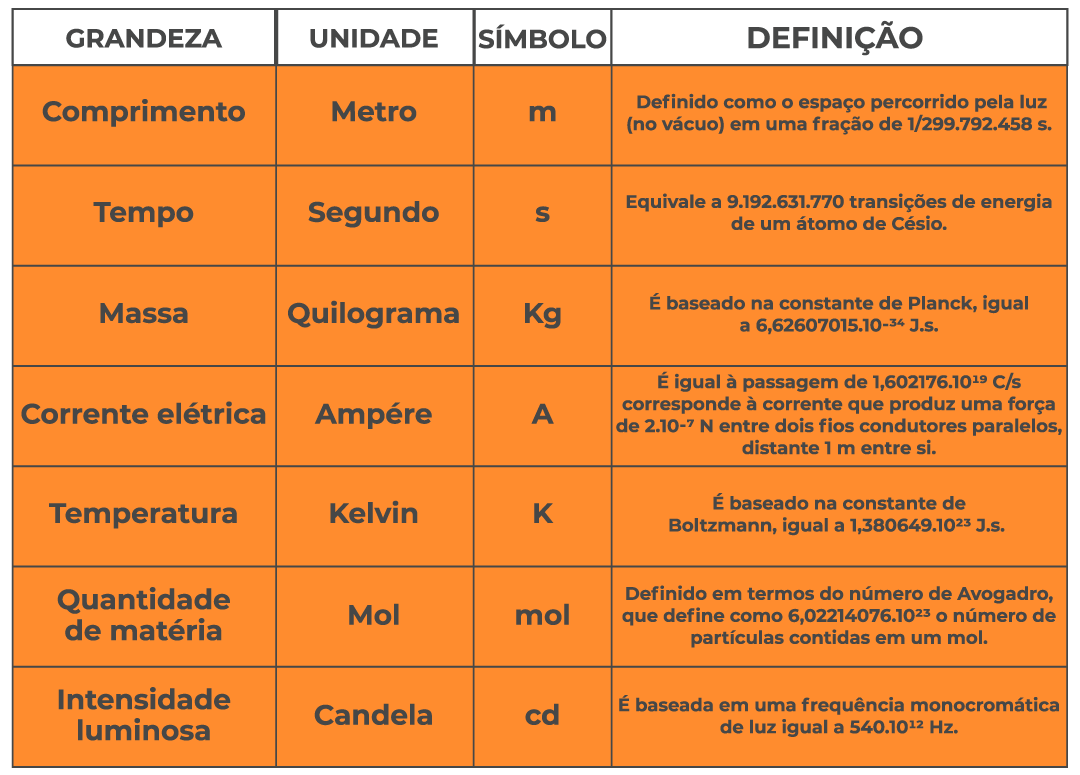
Em 1971, a 14ª Conferência Geral de Pesos e Medidas escolheu sete grandezas como fundamentais, formando assim, a base do Sistema Internacional de Unidades (SI), popularmente conhecido como sistema métrico. As principais grandezas fundamentais, que utilizamos cotidianamente, são o comprimento, a massa e o tempo.
Os Estados Unidos são um dos poucos países que ainda não adotaram oficialmente o Sistema Internacional de Unidades.
MEDIDA DE COMPRIMENTO: O METRO
O metro foi definido inicialmente em termos da distância entre o Pólo Norte e o Equador. Hoje em dia, é definido como a distância percorrida pela luz durante um certo intervalo de tempo.
MEDIDA DE TEMPO: O SEGUNDO
O segundo foi definido inicialmente em termos da rotação da Terra. Hoje em dia, é definido em termos das vibrações da luz emitida por um átomo de césio-133.
MEDIDA DE MASSA: O QUILOGRAMA
O quilograma é definido em termos de um padrão de platina-irídio mantido na França. Para medições em escala atômica, é usada em geral a unidade de massa atômica, definida em termos do átomo de carbono-12.
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
A Notação Científica
Para expressar os números muito grandes e muito pequenos usamos a chamada notação científica, que utiliza potências de 10. Nesta notação, escrevemos $$ 3.560.000.000 m = 3,56 \times 10^{9} m$$ e $$0,000000492 s = 4,92 \times 10^{-7} s ,$$ que também pode aparecer escritas como $$3,56E9 \;\;m $$ e $$4,92E-7\;\; s, $$ respectivamente, onde o E significa “expoente de dez”.
Ainda pode-se usar prefixos combinados com uma unidade, que será multiplicada pelo fator correspondente do prefixo, como, exemplo, giga e nano, que são populares atualmente.
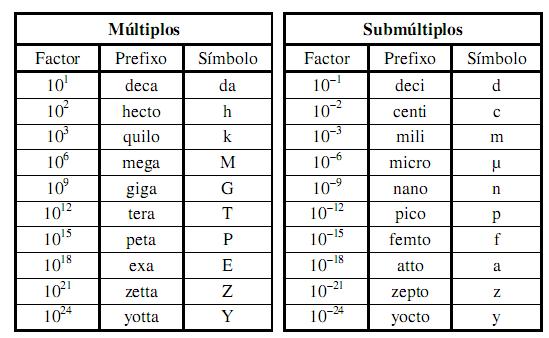
Mudanças de Unidades
Frequentemente é necessário mudar as unidades em que está expressa uma grandeza física. Para isso, usamos um método chamado de conversão em cadeia. Neste método, multiplicamos a medida original por um fator de conversão, o que nos leva entender que o número e sua unidade formam um todo, e as unidades obedecem às mesmas regras que os números e as variáveis algébricas. Gerando assim a igualdade $$ \frac{1 \text{ min } }{60 s} = 1 \qquad e \qquad \frac{60s}{1 \text{ min } } = 1.$$
EXEMPLO: Quantos centímetros tem uma área de 6,0 km²?
Note que $$ 6,0 km^2 = 6,0 (km)(km) = 6,0(1000m)(1000m) = 6,0 \times 10^{6}m^2 = \\ = 6,0 \times 10^{6}(m)(m) = 6,0 \times 10^{6}(100 cm)(100 cm) = 6,0 \times 10^{10}cm^2. $$
Referências:
- Halliday, Resnick e Walker. “Fundamentos de Física – Vol. 1: Mecânica” – Link para compra do livro.
- Batschelet. “Introdução à Matemática Para Bio-cientistas” – Link para compra do livro.