Uma função f definida em S é uma regra que associa cada z do conjunto S a um número complexo w, denominado valor de f em z.
Desta forma, escrevemos $$f(z) = w,$$ onde z é denominada variável complexa, o conjunto S é o domínio da função f.
Neste contexto, queremos, nesse artigo, estabelecer conceitos de limite e continuidade inerentes ao cálculo, agora, para funções complexas.
Limite de Uma Função Complexa
Antes de definir o conceito de limite para uma função complexa, precisamos definir o conceito de discos no plano complexo.
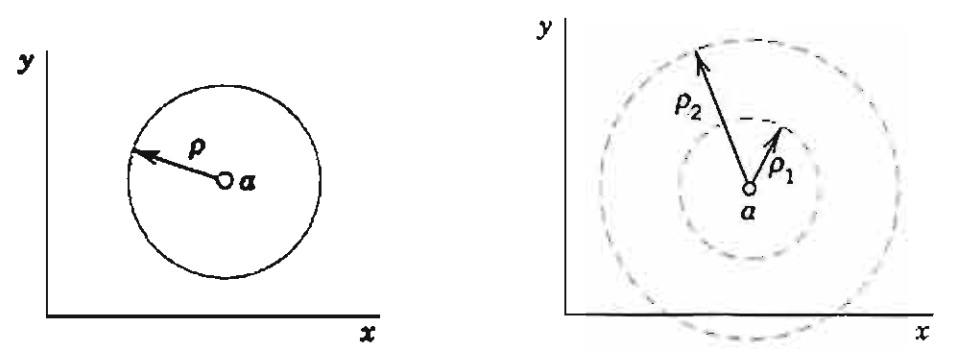
Dados os números r>0 e z_0 um número complexo qualquer, denomina-de disco aberto com centro em z_0 = x_0 + i y_0 e raio r o conjunto D_r (z_0), de números complexos, dados por $$D_r (z_0) = \{ z; |z-z_0| < r \} = \{ x+yi; \sqrt{(x-x_0)^2 + (y-y_0)^2} < r \}.$$
O disco fechado com centro em z_0 = x_0 + i y_0 e raio r é o conjunto $$ \{ z; |z-z_0| \leq r \}$$ que é formado pelos pontos de D_r (z_0) e os pontos da fronteira $$ \{ z; |z-z_0| = r \}.$$
Seja z_0 um ponto de acumulação do domínio D de uma função f. Diz-se que f tem limite L com z tendendo a z_0 se dado qualquer \varepsilon > 0 existe \delta <0 tal que $$z \in D,\;\; 0<|z-z_0|< \delta \Rightarrow |f(z)-L|< \varepsilon .$$
Neste caso, escrevemos $$\lim_{z \rightarrow z_0}{f(z)} = L.$$
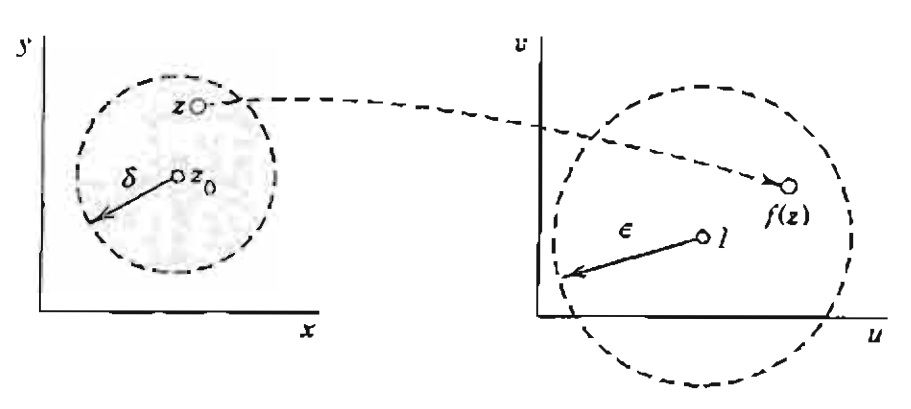 Representação da definição de Limite de Uma Função Complexa
Representação da definição de Limite de Uma Função Complexa
O limite de uma função f(z), se existe, é único
Propriedades dos Limites de Funções Complexas:
Sejam f e g duas funções complexas com limites finitos para z \rightarrow z_0, então
- \lim_{z \rightarrow z_0}{[f(z)+g(z)]} = \lim_{z \rightarrow z_0}{f(z)} +\lim_{z \rightarrow z_0}{g(z)}.
- \lim_{z \rightarrow z_0}{[f(z)g(z)]} = \lim_{z \rightarrow z_0}{f(z)}\lim_{z \rightarrow z_0}{g(z)}.
- \lim_{z \rightarrow z_0}{\frac{f(z)}{g(z)}} = \frac{\lim_{z \rightarrow z_0}{f(z)}}{\lim_{z \rightarrow z_0}{g(z)}} se \lim_{z \rightarrow z_0}{g(z)} \neq 0
- \lim_{z \rightarrow z_0}{\bar{f}(z)} = \bar{\lim_{z \rightarrow z_0}{f(z)}}.
EXEMPLO
$$\lim_{z \rightarrow 2i}{(z^2 + 3z)} = (2i)^2+3(2i) = 4(-1)+6i = -4+6i.$$
EXEMPLO
Usando uma técnica simples do cálculo de limite de funções reais (multiplicar pelo conjugado do denominador) encontramos que
$$\lim_{z \rightarrow 0}{\frac{\sqrt{1+z} -1}{z}} = \frac{1}{2}$$
EXEMPLO
$$\lim_{z \rightarrow 0}{\frac{Re(z^2)}{|z|^2}} = ?$$
Temos uma indeterminação que precisa ser solucionada.
Temos que z^2 =(x^2-y^2) + (2xy)i para todo z=x+iy. Assim, temos que $$ z \rightarrow 0 \Leftrightarrow x\rightarrow 0\;\;\;e\;\;\;y\rightarrow 0.$$ Desta forma,
$$\lim_{z \rightarrow 0}{\frac{Re(z^2)}{|z|^2}} = \lim_{(x,y) \rightarrow (0,0)}{\frac{x^2-y^2}{x^2+y^2}}$$
Neste caso, podemos fazer $$\lim_{(x,y) \rightarrow (0,0)}{f(x,y)} = \lim_{x \rightarrow 0}{f(x,0)}$$ e $$\lim_{(x,y) \rightarrow (0,0)}{f(x,y)} = \lim_{y \rightarrow 0}{f(0,y)}$$ cujos limites devem ser iguais em ambos os casos.
Assim,
$$\lim_{(x,y) \rightarrow (0,0)}{\frac{x^2 – y^2}{x^2 + y^2}} = \lim_{x \rightarrow 0} {\frac{x^2}{x^2}} = 1.$$ e
$$\lim_{(x,y) \rightarrow (0,0)}{\frac{x^2 – y^2}{x^2 + y^2}} = \lim_{y \rightarrow 0} {\frac{- y^2}{ y^2}} = – 1.$$
Portanto, não existe $$\lim_{(x,y) \rightarrow (0,0)}{\frac{x^2 – y^2}{x^2 + y^2}}$$
Portanto, não existe \lim_{z \rightarrow 0}{\frac{Re(z^2)}{|z|^2}}.
Seja a função w=f(z) com domínio S.
Decompondo esta função complexa w em suas partes real e imaginária, teremos:
$$w = u(x,y) + iv(x,y)$$, sendo u=u(x,y) e v=v(x,y) funções reais, definidas no subconjunto
S, agora sendo um conjunto do plano \mathbb{R}^2.
Desse modo, uma condição necessária e suficiente para que $$\lim_{z \rightarrow z_0}{f(z)} = a + bi$$ é que $$\lim_{(x,y) \rightarrow (x_0,y_0)}{u(x,y)}=a\;\;\;e\;\;\;\lim_{(x,y) \rightarrow (x_0,y_0)}{v(x,y)}=b$$ considerando z_0 = x_0 + y_0 i.
Esta forma de decomposição é utilizada para mostrar que algumas funções complexas não possuem limite em algum ponto, isto é feito considerando que o limite quando existe é único, então se exibirmos para uma dada função dois limites diferentes quando tomamos caminhos diferentes estaremos mostrando que o limite não existe.
EXEMPLO $$\lim_{z \rightarrow 0}{\frac{|z|}{z}} = ?$$
$$\lim_{z \rightarrow 0}{\frac{|z|}{z}} = \lim_{z \rightarrow 0}{\frac{|z| \bar{z} }{z \bar{z}}} = \lim_{(x,y) \rightarrow (0,0)}{\frac{x\sqrt{x^2+y^2} – i y \sqrt{x^2+y^2} }{x^2 + y^2}}=$$ $$= \lim_{(x,y) \rightarrow (0,0)}{\frac{x\sqrt{x^2+y^2} }{x^2 + y^2}} – i \lim_{(x,y) \rightarrow (0,0)}{\frac{y \sqrt{x^2+y^2} }{x^2 + y^2}}.$$
Como nenhum dos limites das funções $$u(x,y) = \frac{x\sqrt{x^2+y^2} }{x^2 + y^2}; \;\;\; v(x,y) = \frac{y \sqrt{x^2+y^2} }{x^2 + y^2}$$ existe, então, o limite $$\lim_{z \rightarrow 0}{\frac{|z|}{z}}$$ também não existe.
Limites Infinitos Para Funções Complexas
Assim como nas funções reais, podemos definir limites que tendem a infinito ou funções cujos limites são infinitos mesmo quando suas variável tende a uma constante complexa. Estes casos serão exemplificados abaixo.
EXEMPLO $$\lim_{z \rightarrow 4i}{\frac{5z}{2z-8i}} = ?$$
Temos que
\begin{eqnarray*}
\frac{5z}{2z-8i} & = & \frac{5z}{2(z-4i)}\\
& = & \frac{5}{2} \frac{z}{(z-4i)}\\
& = & \frac{5}{2} \frac{x+iy}{(x+iy-4i)}\\
& = & \frac{5}{2} \frac{x+iy}{(x+i(y-4))}\\
& = & \frac{5}{2} \frac{x+iy}{(x+i(y-4))} \frac{(x-i(y-4))}{(x-i(y-4))}\\
& = & \frac{5}{2} \frac{(x+iy)(x-i(y-4))}{(x^2+(y-4)^2)}\\
& = & \frac{5}{2} \frac{(x^2+y(y-4)) + (xy – x(y-4))i}{(x^2+(y-4)^2)}\\
& = & \frac{5}{2} \frac{(x^2+y(y-4))}{(x^2+(y-4)^2)} + \frac{5i}{2} \frac{(xy – x(y-4))}{(x^2+(y-4)^2)}\\
\end{eqnarray*}
Ou seja,
$$\lim_{z \rightarrow 4i}{\frac{5z}{2z-8i}} = \frac{5}{2} \lim_{(x,y) \rightarrow (0,4)} \frac{(x^2+y(y-4))}{(x^2+(y-4)^2)} + \frac{5i}{2} \lim_{(x,y) \rightarrow (0,4)} \frac{(xy – x(y-4))}{(x^2+(y-4)^2)}.$$
Fazendo x=\alpha t e y=\beta t + 4 temos que,
$$\lim_{z \rightarrow 4i}{\frac{5z}{2z-8i}} = + \infty$$
EXEMPLO $$\lim_{z \rightarrow \infty}{\frac{1}{z}} = ?$$
$$\lim_{z \rightarrow \infty}{\frac{1}{z}} = \lim_{z \rightarrow \infty}{\frac{\bar{z}}{z. \bar{z}}} = \lim_{z \rightarrow \infty}{\frac{\bar{z}}{|z|^2}}= \lim_{(x,y) \rightarrow (\infty, \infty)}{\frac{x}{x^2 + y^2}}+ i \lim_{(x,y) \rightarrow (\infty, \infty)}{\frac{y}{x^2 + y^2}}.$$
Fazendo x= \alpha t e y=\beta t, temos que $$\lim_{(x,y) \rightarrow (\infty, \infty)}{\frac{x}{x^2 + y^2}}+ i \lim_{(x,y) \rightarrow (\infty, \infty)}{\frac{y}{x^2 + y^2}} = $$ $$ = \lim_{t \rightarrow \infty}{\frac{\alpha t}{t^2(\alpha^2 + \beta^2)}}+ i \lim_{t \rightarrow \infty}{\frac{\beta t}{t^2(\alpha^2 + \beta^2)}}=0+0i=0$$
Agora, com este resultado, podemos enxergar algumas funções complexas de maneira similar a que enxergamos uma função real para o cálculo dos limites.
Vamos fazer isso no próximo exemplo:
EXEMPLO: $$\lim_{z \rightarrow \infty}{\frac{3iz +5}{2z-i}} = ?$$
$$\lim_{z \rightarrow \infty}{\frac{3iz +5}{2z-i}} = \lim_{z \rightarrow \infty}{\frac{\frac{3iz}{z} +\frac{5}{z}}{\frac{2z}{z}-\frac{i}{z}}}=\frac{3i}{2}$$
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
EXEMPLO
$$\lim_{z \rightarrow \infty}{\frac{z^2-i}{3z+5}} = \infty $$
Continuidade de Funções Complexas
Quando o ponto z_0 pertence ao domínio de f e L = f(z_0), dizemos que f é contínua no ponto z_0 e escrevemos $$\lim_{z \rightarrow z_0}{f(z)} = f(z_0).$$
A função f é dita contínua em um conjunto S \subset \mathbb{C} se é contínua em cada um dos pontos deste conjunto S.
EXEMPLO Considere a função $$f(x,y) = \left\{ \begin{array}{lll}
0; & z=2+i\\
\frac{z+3i}{2}; & z \neq 2+i
\end{array}
\right.
$$
Vamos verificar se f é contínua no ponto z=2-i.
Como $$lim_{z \rightarrow 2-i}{\frac{z+3i}{2}} = 1+i$$ então essa função não é contínua em z=2-i.
PROPRIEDADES DA CONTINUIDADE
Sejam f e g duas funções complexas contínuas no ponto z_0, então
- [f(z)+g(z)] é contínua em z_0.
- [f(z)- g(z)] é contínua em z_0.
- [f(z)g(z)] é contínua em z_0.
- \frac{f(z)}{g(z)} é contínua em z_0, desde que g(z_0) \neq 0.
EXEMPLO Considere f(z) = \left\{ \begin{array}{rl}|z|^2 Re(1/z); & z \neq 0\\\\0; & z=0 \\\end{array} \right.
Como $$\frac{1}{z} = \frac{\bar{z}}{z.\bar{z}}=\frac{\bar{z}}{x^2+y^2} = \frac{x}{x^2+y^2} -i\frac{y}{x^2+y^2},$$ então $$f(z) = f(x+iy) = (x^2+y^2) \frac{x}{x^2+y^2} = x.$$
Assim, f(z) é uma função da variável complexa a valores reais e $$\lim_{z\rightarrow 0}{f(z)} = \lim_{x\rightarrow 0}{x} = 0.$$ Portanto, $$\lim_{z\rightarrow 0}{f(z)}=f(0),$$ou seja, f é contínua no ponto z=0.
TEOREMA
Uma função f(z) = u(x,y) + iv(x,y) é contínua num ponto z_0 = x_0 + i y_0 se, e somente se u(x,y) e v(x,y) são contínuas no ponto (x_0, y_0).
EXEMPLO Considere f(z) = \left\{ \begin{array}{rl}\frac{|z|}{z}; & z \neq 0\\\\0; & z=0 \\\end{array} \right. f é contínua no ponto z=0?
Como vimos anteriormente o limite \lim_{z \rightarrow 0}{\frac{|z|}{z}} não existe, logo a função f(z) não pode ser contínua em z=0.
Leia Mais:
- Funções de Variáveis Complexas | Uma Introdução.
- Números Complexos | Primeiras Definições e Operações Elementares
- Números Complexos | A Forma Polar e as Operações Elementares
- Números Complexos | A Exponencial de um Número Complexo


