Uma função é seccionalmente contínua, ou contínua por partes, em um intervalo se tem no máximo em número finito de descontinuidades finitas.

A noção de função contínua é um dos pontos centrais da Topologia, por consequência, assim também são as funções contínuas por partes, ou seccionalmente contínuas, que, grosso modo, são aquelas funções com uma quantidade enumerável de pontos de descontinuidade, ou seja, é contínua em cada partição pré-estabelecida do seu domínio. As funções seccionalmente contínuas, ou contínuas por partes, são essenciais para os teoremas de convergência das séries de Fourier e das Transformadas Integrais.
De modo mais rigoroso, diz-se que uma função f(x) é seccionalmente contínua em um intervalo se
Você precisa passar em cálculo? Não se preocupe, nós podemos ajudar! Clique aqui e descubra como podemos facilitar sua aprovação. |
(i) o intervalo pode ser subdividido em um número finito de subintervalos em cada um dos quais f(x) é contínua; e
(ii) os limites laterais de f(x) , quando x tende para os pontos extremos desses subintervalos, são finitos.
Outra maneira de formular a definição é:
Uma função é seccionalmente contínua em um intervalo se tem aí no máximo em número finito de descontinuidades finitas.
Observação:
- Todas as funções contínuas na reta real é seccionalmente contínua.
- Note que não é necessário que a função esteja definida nos pontos extremos da partição. Isso porque, um ponto pode ser descontinuidade de uma função, mesmo que ele não pertença ao domínio de f . A rigor não deveria ser assim, mas é natural considerarmos o que se passa nas proximidades de pontos de acumulação do domínio de uma função, mesmo que tais pontos não pertençam ao domínio;
- Na maioria das vezes, as descontinuidades de funções seccionalmente contínuas serão de primeira espécie, ou seja, quando os limites laterais distintos.
A figura abaixo ilustra um exemplo da função seccionalmente contínuas.
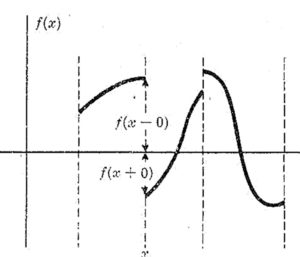 Exemplo de Função seccionalmente contínua
Exemplo de Função seccionalmente contínua
Exemplo de uma Função Seccionalmente Contínua (A Função de Heaviside)
A função de Heaviside ou função degrau unitário, desenvolvida pelo matemático e engenheiro eletricista Oliver Heaviside é simples de ser definida, pois é nula para argumento negativo e vale 1 para argumento positivo.
Esta função é frequentemente encontrada em engenharia, nos problemas que podem apresentar dualidade como “ligado” ou “desligado”.
Assista uma vídeo-aula deste conteúdo: Clique aqui e confira a aula pelo Youtube
Esta função degrau unitário é denotada por u(t-a) e dada por:
$$u(t-a) = \left\{ \begin{array}{lll}
0 & ; & t<a\\
1& ; & t \geq a\\
\end{array} \right. \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;a \geq 0.$$
O gráfico da função degrau é dado por:
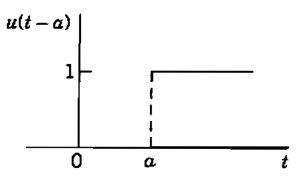 Gráfico da Função Degrau Unitário ou de Heaviside
Gráfico da Função Degrau Unitário ou de Heaviside
Se a = 0 esse gráfico é:
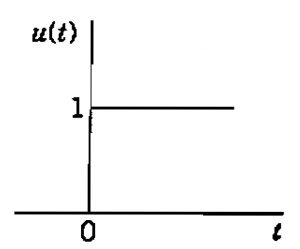 Função Degrau Unitário ou de Heaviside com a=0
Função Degrau Unitário ou de Heaviside com a=0
Esta função é seccionalmente contínua pois pode ser dividida em duas partes partes contínuas, sendo x = 0 seu único ponto de descontinuidade.
Exemplos de funções periódicas e seccionalmente contínuas
1) Faça o gráfico de cada uma das seguintes funções:
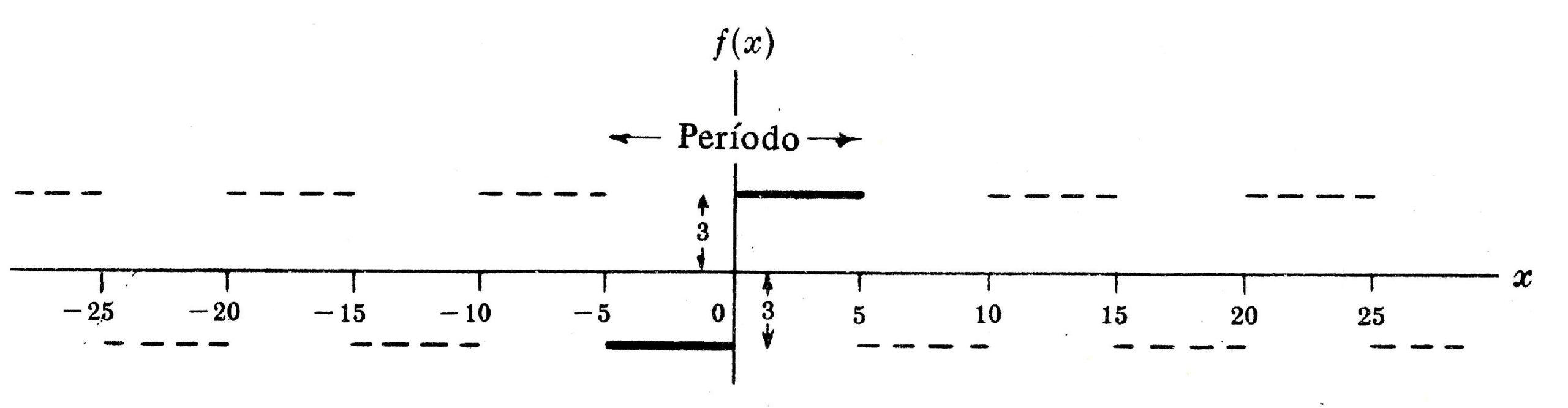
a) f(x) = 3 , se 0 < x < 5 , f(x) = - 3 , se -5 < x < 0 e f(x +10) = f(x).
SOLUÇÃO: Como o período é 10, a porção do gráfico em -5 < x < 5, representa por traço cheio na figura, se repete periodicamente fora desse intervalo (gráfico tracejado). Note-se que f(x) não é definida em x = 0, 5, -5, 10, -10, 15, -15, etc. Esses valores são os pontos de descontinuidade de f(x) .
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
b) f(x) = sen(x) , se 0 \leq x \leq \pi , f(x) = 0 , se \pi < x < 2 \pi e f(x + 2 \pi) = f(x).
SOLUÇÃO: Note que f(x) é definida e contínua para todo x .

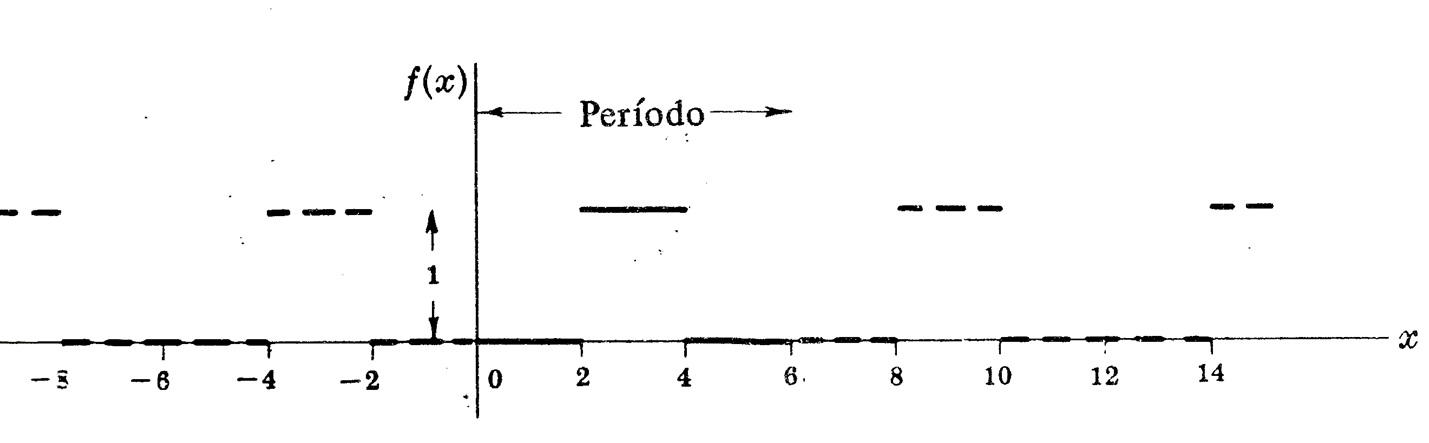
c) f(x) = 0 , se 0 \leq x < 2 , f(x) = 1 , se 2 \leq x < 4 , f(x) = 0 , se 4 \leq x < 6 e f(x +6) = f(x).
SOLUÇÃO:
Leia Mais:
- Séries de Fourier | História, Definição e Condições de Convergência.
- Séries de Fourier | Ortogonalidade das Funções Seno e Cosseno
- O Que São Funções Periódicas? Definição e Exemplos.
- Séries de Fourier | Os Coeficientes de Fourier
- Séries de Fourier de Senos e Cossenos | A Expansão em Meio-Intervalo.


