Neste artigo queremos apresentar uma lista de exercícios sobre as equações diferenciais ordinárias homogêneas de segunda ordem. Pra isso, precisamos encontrar y_1 e y_2 que sejam duas soluções da equação y'' + p(t) y' + q(t)y=0 e que formem um conjunto fundamental de soluções desta equação. Então a combinação linear y(t) = c_1 y_1 +c_2y_2 será a solução geral da equação homogênea, quaisquer que sejam os valores das constantes c_1 e c_2.
Para saber se esta solução y(t) é a solução geral de y'' + p(t) y' + q(t)y=0 precisamos que o determinante Wronskiano ou apenas wronskiano das soluções y_1 e y_2 que é dado por
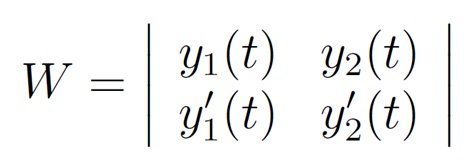
Você precisa passar em cálculo? Não se preocupe, nós podemos ajudar! Clique aqui e descubra como podemos facilitar sua aprovação. |
seja diferente de zero para algum ponto do intervalo de continuidade dos coeficientes.
E.D.O.’s Homogêneas de 2ª Ordem | 1ª Lista de Exercícios Resolvidos
1) Encontre um CFS da Equação y'' + y = 0
SOLUÇÃO: Primeiramente vamos encontrar a solução da equação homogênea associada y'' + y = 0:
$$y” + y= 0 \Rightarrow \lambda ^2 + 1 = 0 \Rightarrow \lambda _1 =i\;\;e\;\; \lambda _2 = -i.$$
Logo, $$y_{H} (t) = c_1 cos(t) + c_2 sen(t).$$
Nesse caso, tomamos y_1(t) = cos(t) e y_2(t) = sen(t) e facilmente podemos ver que W \left( y_1 , y_2 \right) = 1 .
2) Encontre um CFS da Equação y''+9y = 0
SOLUÇÃO: Primeiramente vamos encontrar a solução da equação homogênea associada y'' + 9y = 0:
$$y” + 9y= 0 \Rightarrow \lambda ^2 + 9= 0 \Rightarrow \lambda _1 =3i\;\;e\;\; \lambda _2 = -3i.$$
Logo, $$y_{H} (t) = c_1 cos(3t) + c_2 sen(3t).$$
Nesse caso, tomamos y_1(t) = cos(3t) e y_2(t) = sen(3t) e facilmente podemos ver que W \left( y_1 , y_2 \right) = 3 .
3) y'' - \dfrac{2t}{1+t^2}y' + \dfrac{2}{1+t^2}y = 0
SOLUÇÃO: Como a equação homogênea associada dessa EDO não tem coeficientes constantes deveremos encontrar duas soluções particulares suas que formem um CFS.
Para isso, vamos reescrever a Equação Homogênea Associada como $$y” – \frac{2t}{1+t^2}y’ + \frac{2}{1+t^2}y = 0 \Rightarrow (1+t^2) y” – 2ty’ + 2y = 0.$$
Desta forma, fatalmente as duas soluções particulares terão estruturas polinomiais e testando as formas $$y_{1}(t) = at + b; \;\;\;\;y{2}(t) = at^2 + bt +c$$ encontramos como duas soluções particulares $$y_{1}(t) = t; \;\;\;\;y{2}(t) = t^2 -1.$$
Obviamente, você pode encontrar outras soluções particulares que também formem um CFS como é o caso dessas duas, cujo Wronskiano é dado por $$W(y_1, y_2) = t^2 +1.$$
Assim, $$y(t) = c_1 t + c_2 (t^2 -1) + y_{p}$$.
4) t^2 y'' + ty'+y=0, \;\;\;t>0
SOLUÇÃO: Essa é uma equação de Euler-Cauchy com equação característica dada por $$r^2 +(1-1)r +1 = 0 \Rightarrow r=\pm i.$$
Saiba mais: O que são EDO’s de Euler-Cauchy?
Ou seja, temos raízes complexas conjugadas, o que nos leva à solução $$y(t) = c_1 cos\left( ln(t) \right) + c_1 sen \left( ln(t) \right) $$
5) t^2y'' + 2t y' +2y = 0\;\;\;t>0
SOLUÇÃO: Essa é uma equação de Euler-Cauchy com equação característica dada por $$r^2 +(2-1)r +2 = 0 \Rightarrow r=\frac{1 \pm i \sqrt{7}}{2}.$$
Ou seja, temos raízes complexas conjugadas, o que nos leva à solução $$y(t) = e^{1/2} \left( c_1 cos\left( \frac{\sqrt{7}}{2} \ln(t) \right) + c_1 sen \left( \frac{\sqrt{7}}{2} \ln(t) \right) \right) $$
6) (1-t)y''+ty'-y =0;\;\;\;sabendo\;\;\;que\;\;\;y_{1}(t) = t.
SOLUÇÃO: Sabemos que y_1 (t) = t e que y_H (t) = c_1 t + c_2 y_2 (t).
Podemos usar o método da redução de ordem para encontrar y_2(t) , mas usando o forçamento da EDO como inspiração, vou testar se e^{at} pode ser uma forma de solução.
Saiba Mais: O que é o Método da Redução de Ordem?
Observe que \left( e^{at} \right) ' = a e^{at} e \left( e^{at} \right)''= a^2 e^{at} .
Substituindo na EDO homogênea associada encontramos:
$$(1-t) a^2 e^{at} + a e^{at} t – e^{at} = e^{at} \left( [1-t]a^2 + at -1 \right) = 0.$$
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
Como e^{at} \neq 0, \forall t \in \mathbb{R} , então $$\left( [1-t]a^2 + at -1 \right) = 0$$ e isso acontece sempre que a=1 , independente do valor de t .
Logo, encontramos y_2 (t) = e^t .
Portanto, encontramos $$y_H (t) = c_1 t + c_2 e^t ,$$ pois W(t, e^t) = e^t (t-1) .
7) t^2y''+ty'-y = 0, t>0.
SOLUÇÃO: A EDO homogênea Euler-Cauchy. Assim, a equação característica da EDO t^2y''+ty'-y = 0 é dada por r^2 -1 = 0 , o que nos dá a solução: $$y_H (t) = c_1 t + c_2 t^{-1} .$$ Portanto, y_1 (t) = t e y_2 (t) = t^{-1} e W(t, t^{-1}) = -2 t^{-1} .
8) Estabeleça Um conjunto fundamental de soluções da EDO homogênea y''+y = 0 .
SOLUÇÃO: A EDO homogênea y''+y = 0 , possui equação característica \lambda ^2 +1 = 0 , que tem raízes complexas conjugadas dadas por \lambda = \pm i , ou seja, $$y_H (t) = c_1 cos(t) + c_2 sen (t) .$$
Portanto, \{ cos(t), sen(t) \} é um conjunto fundamental de soluções da equação homogênea associada.
9. Determine um Conjunto Fundamental de Soluções e uma solução geral de y'' + k^2 y = 0 , sendo k uma constante real.
SOLUÇÃO: A equação característica neste caso é dada por $$ m^2 + k^2 = 0$$ e tem raízes $$m_1 = i k \;\;\;e \;\;\; m_2 = -i k .$$ Portanto, uma solução geral, neste caso é dada por $$y(x) = c_1 cos(kx) + c_2 sen(kx).$$
Desta forma, um Conjunto Fundamental de Soluções desta equação é dado por $$ \{ cos(kx) , sen(kx) \}, $$ desde que k = 0 , pois $$ W(cos(kx), sen(kx)) = kcos^2 (kx) + k sen^2 (kx) = k.$$
LEIA MAIS:
- Equações Diferenciais Ordinárias de 2ª Ordem, Homogêneas, com Coeficientes Constantes
- Variação dos Parâmetros: EDOs de 2ª Ordem Linares
- Equações Diferencias Ordinárias de 2ª Ordem: Método dos Coeficientes Indeterminados
- Equações Diferencias Ordinárias de 2ª Ordem: O Princípio da Superposição
- Solucionando EDO’s por Transformada de Laplace | Exercícios Resolvidos



Pingback: EDOs de 2ª Ordem: Equações Homogêneas | Matemática Simplificada