O sistema de equações de Nagumo-Fitzhugh é um dos principais modelos matemáticos que descrevem os padrões com os quais potenciais de ação são iniciados e propagados nos neurônios.

A neurodinâmica refere-se à comunicação entre diferentes partes do sistema nervoso e à relação do sistema nervoso com o sistema músculo-esquelético. Foi demonstrado que os nervos se movem independentemente de outros tecidos.
O termo Neurodinâmica apareceu pela primeira vez em 1989 e, desde então, foi desenvolvido. A neurodinâmica é agora vista como uma parte importante da avaliação e tratamento de lesões.
Você precisa passar em cálculo? Não se preocupe, nós podemos ajudar! Clique aqui e descubra como podemos facilitar sua aprovação. |
De uma maneira simplificada, o sistema modelado que descreve o comportamento dos impulsos elétricos de células neurais se assemelha a sistemas elétricos. Nada mais natural, visto que um neurônio é uma célula do corpo que recebe estímulos elétricos que são conduzidos ao longo do axônio, um componente da célula nervosa que pode ser comparado a um cabo elétrico que se conecta a outros neurônios.
Os circuitos elétricos muitas vezes são governados por equações diferencias, desde as mais simples até os modelos matemáticos não-lineares mais complexos. Estes circuitos são elementos rotineiros em pesquisas nas áreas de engenharia e queremos familiarizar o agora aluno e futuro profissional (e pesquisador) da área com algumas técnicas matemáticas utilizadas para analisar qualitativa e quantitativamente os problemas que podem nascer destes circuitos elétricos como objeto de suas futuras pesquisas.
Equações diferencias ordinárias mais simples, como as de primeira ordem, podem descrever circuitos elétricos como o circuito RL (que é obtido utilizando a segunda lei de Kirchhoff e a lei de Ohm). Um segundo exemplo simples é o modelo do fluxo de corrente no circuito ilustrado na figura abaixo:
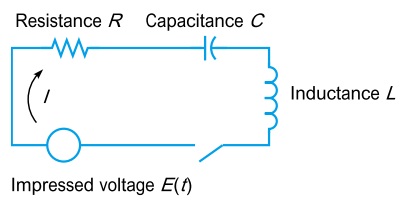
Contudo, nosso problema do sistema de equações de Nagumo-Fitzhugh consiste de um sistema não linear. Assim, iremos buscar inspiração em problemas já conhecidos e clássicas aplicações da teoria das equações diferenciais ordinárias não-lineares no campo dos circuitos elétricos.
Estudos prévios da Equação de Lienard e da Equação de van der Pol irão nos mostrar o caminho a ser percorrido para a realização da análise do sistema de equações de Nagumo-Fitzhugh. Para que este caminho seja seguido serão necessários alguns alicerces teóricos acerca da teoria das equações diferenciais ordinárias não-lineares que não fazem parte da grade curricular de um curso usual introdutório de Equações Diferenciais, mas que são de grande importância na pesquisa principalmente pesquisas no campo da engenharia. Sendo assim, é indispensável um estudo que abrange a teoria da análise qualitativa de sistemas autônomos lineares (planos e espaços de fase e estabilidade).
Como a matemática ajudou a desenvolver o estudo da Neurodinâmica
Um dos maiores avanços no estudo dos impulsos elétricos gerados por células nervosas foi o modelo desenvolvido por Hodgkin and Huxley. Em meados do século passado eles criaram um modelo matemático para este fenômeno que trazia um sistema de equações diferenciais de quatro dimensões que descrevia a transmissão eletroquímica de sinais neurais ao longo de uma membrana celular, um trabalho que veio a receber um prêmio Nobel.
De uma maneira simplificada, o sistema modelado que descreve o comportamento dos impulsos elétricos de células neurais se assemelha a sistemas elétricos. Nada mais natural, visto que um neurônio é uma célula do corpo que recebe estímulos elétricos que são conduzidos ao longo do axônio, um componente da célula nervosa que pode ser comparado a um cabo elétrico que se conecta a outros neurônios.
É claro que o movimento não é realmente elétrico, pois a corrente não é composta por elétrons, mas sim por ions (com predominância de sódio e potássio). Entretanto, alheio ao estudo da neurobiologia, nosso foco principal seria discutir o sistema de equação diferenciais estabelecido na pesquisa de Hodgkin and Huxley, mas a alta não-linearidade deste sistema torna-o um problema complexo de se lidar por um pesquisador iniciante.
Um avanço do ponto de vista matemático foi alcançado por Fitzhugh e Nagumo que conseguiram um modelo mais simples que o modelo de Hodgkin-Huxley. Embora este novo sistema não seja tão biologicamente preciso quanto o original, matematicamente ele descreve comportamentos importantes dos impulsos nervosos.
A ideia central é explorar este sistema como faríamos com um sistema elétrico, ou seja, buscar em algum problema já resolvido (como a Equação de van der Pol, por exemplo) caminhos que nos levem a resultados satisfatórios de maneira analítica e posteriormente de maneira numérica.
Para iniciar a modelagem do sistema, devemos antes enfatizar três condições básicas que o potencial deve obedecer para que seja um potencial de ação (PA):
- Deve existir um limiar de voltagem para que um estímulo desencadeie o PA;
- Uma vez atingido o limiar, a voltagem deve aumentar até o máximo possível;
- Caso o estímulo não atinja o limiar, ele deve desaparecer rapidamente.
O Modelo Neurodinâmico de Nagumo-Fitzhugh
O sistema de equações de Nagumo-Fitzhugh é dado por
\begin{equation} \label{Nagumo-Fitz}
\left\{ \begin{array}{lcr}
\dot{x} & = & y+x-\dfrac{x^3}{3}+I\\
\\
\dot{y} & = & -x+a-by
\end{array} \right.
\end{equation}
onde a e b são constantes satisfazendo
\begin{equation} \label{conditions}
0 < \dfrac{3}{2}(1-a)<b<1 \;\;\;\;\;\;\;\; (2)
\end{equation}
e I é um parâmetro chamado de parâmetro de estímulo. Este parâmetro pode ser encarado como uma corrente aplicada induz a excitação do sistema.
Nestas equações a variável x é similar a voltagem e representa a excitabilidade do sistema e a variável y representa a combinação das outras forças que tendem voltar o sistema ao seu estado de repouso.
A ideia central é explorar este sistema como faríamos com um sistema elétrico, ou seja, buscar em algum problema já resolvido (como a Equação de van der Pol, por exemplo) caminhos que nos levem a resultados satisfatórios de maneira analítica e posteriormente de maneira numérica.
A motivação para o modelo de Nagumo-FitzHugh foi isolar conceitualmente as propriedades essencialmente matemáticas de excitação e propagação das propriedades eletroquímicas do fluxo de íons de sódio e potássio. O modelo consiste em uma variável semelhante à voltagem com não linearidade cúbica que permite a autoexcitação regenerativa por meio de um feedback positivo, e uma variável de recuperação tendo uma dinâmica linear que fornece um feedback negativo mais lento.
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
FitzHugh modificou o modelo de van der Pol para explicar as propriedades básicas da excitabilidade. Embora o Modelo Hodgkin-Huxley seja mais realista e biofisicamente sólido, apenas projeções de suas trajetórias de fase quadridimensionais podem ser observadas. A simplicidade do modelo Nagumo-FitzHugh permite que toda a solução seja visualizada de uma só vez. Isso permite uma explicação geométrica de importantes fenômenos biológicos relacionados à excitabilidade neuronal e ao mecanismo de geração de picos.
Pouco depois da publicação das equações de Hodgkin e Huxley, Richard FitzHugh estava trabalhando no Laboratório de Biofísica do National Institutes of Health (NIH) em Bethesda, Maryland. Ele empreendeu uma análise das propriedades matemáticas de suas equações usando as novas técnicas de mecânica não -linear que foram desenvolvidas por matemáticos russos liderados por Andronov.
Isso foi antes de os computadores digitais se tornarem acessíveis. John Moore e FitzHugh começaram planejando como programar um computador analógico que poderia ser usado para resolver as equações de Hodgkin-Huxley. Com esse computador rudimentar, ele traçou soluções para as equações de Hodgkin-Huxley. A operação do computador analógico exigia a habilidade de um engenheiro eletrônico, bem como a de um matemático.
Por sugestão de seu chefe de laboratório, Dr. Kenneth S. (Kacy) Cole, FitzHugh modificou as equações de van der Pol para o oscilador de relaxamento não linear. O resultado tinha um estado de repouso estável, do qual poderia ser excitado por um estímulo elétrico suficientemente grande para produzir um impulso. Um estímulo de corrente constante suficientemente grande produziu uma série de impulsos (FitzHugh 1961,1969).
Mais ou menos na mesma época, um circuito eletrônico foi construído pelo engenheiro japonês Jin-Ichi Nagumo, usando diodos de túnel (Esaki). Esses diodos têm uma curva de corrente-tensão semelhante à forma cúbica usada nas equações de FitzHugh. Desde então, essas equações se tornaram conhecidas como equações de Nagumo-FitzHugh, embora tenham sido originalmente chamadas de “modelo de Bonhoeffer-van der Pol” por FitzHugh. Reprogramar o computador analógico para as equações de Nagumo-FitzHugh foi muito mais simples.
Desde a primeira apresentação do modelo de FitzHugh, o trabalho em neurociência matemática, comunidades inteiras de matemáticos, físicos e engenheiros que estudam a dinâmica não linear de sistemas biológicos evoluíram, mas o modelo Nagumo-FitzHugh permaneceu o exemplo prototípico de um sistema excitável e novas descobertas com esse sistema ainda estão sendo feitas.


