Fórmulas Algébricas: Fatoração de Polinômios e Produtos Notáveis

Abaixo, trazemos as principais fórmulas algébricas, de fatoração polinomiais a produtos notáveis.

Quando falamos de Álgebra, logo pensamos em expressões algébricas, operações algébricas, equações, inequações, produtos notáveis, polinômios e funções, e são a elas que vamos nos ater aqui, enumerando as principais fórmulas de fatoração de polinômios e produtos notáveis especiais.

Fatoração de Polinômios

1) (x-a)^2 = x^2 - 2ax+a^2 ;

2) (x+a)^2 = x^2 + 2ax+a^2 ;

3) (x+a)^3 = x^3 + 3ax^2 +3a^2 x+a^3 ;

4) (x-a)^3 = x^3 - 3ax^2 +3a^2 x - a^3 ;

5) (x+y+z)^2 = x^2+y^2+z^2+2xy+2yz+2zx ;

6) (w+x+y+z)^2 =w^2 +x^2 + y^2 +z^2 +2w(x+y+z)+2x(y+z)+2yz ;

7) a^3+b^3+c^3-3abc = (a+b+c)\times (a^2+b^2+c^2-ab-bc-ca) ;

8) Se a+b+c = 0 então a^3 + b^3 +c^3 = 3abc ;

Produtos Notáveis

Produtos notáveis são multiplicações em que os fatores são polinômios. Existem cinco produtos notáveis mais relevantes: quadrado da soma, quadrado da diferença, produto da soma pela diferença, cubo da soma e cubo da diferença.

1) (x-a)(x+a) = x^2 - a^2 ;

2) (x-a)(x^2+xa+a^2) = x^3 - a^3 ;

3) (x-a)(x^2-xa+a^2) = x^3 + a^3 ;

4) (x-a)(x+a)(x^2+a^2) = x^4 - a^4;

5) (x^2+xa+a^2)(x^2-xa+a^2) = x^4+x^2a^2+a^4 ;

6) Se n é um número natural, então (x-a)(x^{n-1} + a x^{n-2} +a^2 x^{n-3} + ... + a^{n-1}) = x^n - a^n ;

7) Se n é um número natural par, então (x+a)(x^{n-1} + a x^{n-2} +a^2 x^{n-3} + ... + a^{n-1}) = x^n - a^n ;

8) Se n é um número natural ímpar, então (x+a)(x^{n-1} + a x^{n-2} +a^2 x^{n-3} + ... + a^{n-1}) = x^n + a^n ;

OBSERVAÇÃO: O produto (a + b)² = (a + b) ∙ (a + b) =  a² + 2ab + b², interpretado geometricamente abaixo, significa que o quadrado da soma de dois termos é igual ao quadrado do primeiro termo, mais duas vezes o produto do primeiro pelo segundo, mais o quadrado do segundo.

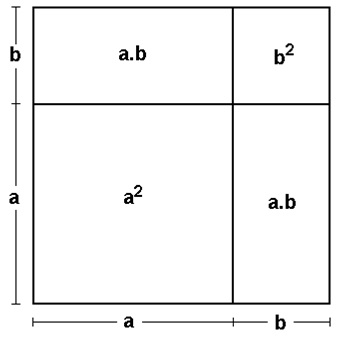
Da mesma forma, poderíamos considerar (a – b)² = (a – b) ∙ (a – b) =  a² – 2ab + b², que significa que o quadrado da diferença de dois termos é igual ao quadrado do primeiro termo, menos duas vezes o produto do primeiro pelo segundo, mais o quadrado do segundo; ou ainda, (a – b) ∙ (a + b) =  a² – b², que significa que o produto da soma de dois termos pela diferença dos mesmos termos é igual ao quadrado do primeiro menos o quadrado do segundo. Uma outra forma de produto notável é a distribuição, o que é caracterizada pelo produto de um fator simples por uma soma ou subtração de dois outros termos deste modo a ∙ (b + c).

Outros Resultados Importantes

1) x^2 + a^2 = (x+a)^2 - 2ax = (x-a)^2 +2ax ;

2) x^3 + a^3 = (x+a)^3 - 3ax (x+a) ;

3) x^3 - a^3 = (x-a)^3 + 3ax (x-a) ;

4) (x+a)^2  = (x-a)^2 +4ax ;

5) (x-a)^2  = (x+a)^2 - 4ax ;

6) (x+a)^2  + (x-a)^2=2 (x^2 +a^2) ;

7) (x+a)^2  - (x-a)^2=4ax ;

8) (x+a)^3  + (x-a)^3=2 x(x^2 +3a^2) ;

9) (x+a)^3  - (x-a)^3=2 a(3x^2 +a^2) ;

10) x^2 + \dfrac{1}{x^2} = \left( x + \dfrac{1}{x} \right)^2 -2 ;

O que são Expressões Algébricas?

Um primeiro ponto a destacar sobre as expressões algébricas é como elas são classificadas, e esta categorização é dada de acordo com a disposição de suas variáveis. Se as variáveis da expressão algébrica aparecem dentro de um radical, então a expressão receberá o nome de irracional, por exemplo, \sqrt{x+1} ; se as variáveis da expressão algébrica não aparecem dentro de um radical, então a expressão receberá o nome de racional, por exemplo, 2x² + 3x + 5; as variáveis poderiam ainda aparecer no denominador de uma expressão algébrica e, neste caso, a expressão receberia o nome de fracionária, por exemplo, \dfrac{x^3}{x+3} .

Após classificar as expressões algébricas, o próximo passo será olhar para os elementos que a compõem. Cada elemento, termo de uma expressão algébrica, recebe o nome de monômio. Voltemos aos três primeiros exemplos: 9z é um monômio, pois é formado pela multiplicação de um número real por uma letra; já r + x possui dois monômios, r e s, por isso recebe o nome de binômio; a expressão algébrica 2x² + 3x + 5 possui três monômios (2x², 3x e 5) logo recebe o nome de trinômio. Se a expressão algébrica tem dois ou mais termos, ela recebe o nome de polinômio.

Apenas para não deixar dúvida, cada termo de uma expressão algébrica é composto de um produto de número por uma ou mais incógnitas , e cada um destes termos ou monômios é separado por um sinal de adição ou subtração.

Em um monômio ou polinômio poderíamos destacar outro elemento, que é seu grau. No caso do monômio, o grau é dado pela soma dos expoentes das letras. Como? Nos exemplos 9z e 13xy²z, os graus dos monômios são respectivamente um e quatro. Já no caso dos polinômios, o grau é dado pelo termo de maior grau. Assim, em r + s o grau é um e em 2x² + 3x + 5 o grau é dois.

Dando continuidade ao nosso estudo sobre as expressões algébricas, temos os termos semelhantes, que são os monômios que possuem a mesma parte literal. Para simplificar, reduzimos a um só termo. A expressão algébrica 2x² + 3x + 5x + x² possui termos semelhantes que podem ser agrupados, reduzidos, simplificados. Reduzindo os termos semelhantes, temos a expressão 3x² + 8x + 5.

Leia Mais:

• O que são Expressões Algébricas? | Matemática Básica
• Trigonometria | Lista de Propriedades Trigonométricas
• Tabela de Derivadas e Integrais
• Tabela Completa de Transformada de Laplace