Desvende o mistério das curvas planas e retas tangentes com este exercício de Cálculo 2. Vamos juntos calcular a área de um triângulo formado por uma circunferência e seus pontos de tangência, revelando as sutilezas da matemática.
Introdução
No vasto universo do Cálculo 2, curvas planas e retas tangentes são como velhos amigos: estão sempre por perto, prontos para te desafiar. Imagine uma circunferência traçando seu caminho pelo plano, e de repente, uma reta ousada toca nela, formando um triângulo com os eixos coordenados.
É como se a matemática estivesse nos convidando para uma dança geométrica, onde cada passo – ou melhor, cada derivada – revela uma nova faceta desse fascinante exercício. E o melhor? Vamos decifrar juntos como calcular a área desse triângulo, desvendando segredos que só as funções vetoriais podem nos contar. Então, pronto para embarcar nessa jornada?
Você precisa passar em cálculo? Não se preocupe, nós podemos ajudar! Clique aqui e descubra como podemos facilitar sua aprovação. |
Exercício
Considere a circunferência descrita pela função vetorial $$\vec{f(t)} = \left( \text{cos}(t), \text{sen}(t) \right), \qquad \text{e} \qquad 0 < \theta < \frac{\pi}{2}.$$ Considere, agora, a reta r tangente a esta circunferência no ponto T \left( \text{cos}(\theta), \text{sen}(\theta) \right) . Considere O como sendo a origem do plano cartesiano, e A e B os pontos de interseção de r com os eixos coordenados. Mostre que a área do triângulo AOB é $$ \text{Área}_{AOB} = \frac{1}{\text{sen}(2 \theta) }.$$
Bases Teóricas Para Solucionar o Exercício:
Uma função vetorial é, por muitas vezes, denominada de curva, pois a representação dada por $$ \vec{f}(t) = x(t) \vec{i} + y(t) \vec{j} = \left( x(t) , y(t) \right) $$ é chamada de representação paramétrica, ou parametrização, da curva C, que é a imagem da função vetorial, e t é chamado de parâmetro desta representação. Este tipo de representação é útil em várias aplicações, por exemplo, em mecânica on a variável t pode ser o tempo.
Parametrização de uma Circunferência:
Um circunferência C com centro em (0, 0) e raio r>0 é uma curva parametrizada como equações paramétricas dadas por $$x(t) = r cost\;\;\;\;y(t) = r \sin{t} \;\;\;\;\;t \in [0, 2 \pi ].$$ Se a circunferência não está centrada na origem, mas no ponto (x_0, y_0) e ainda com raio r>0, então sua parametrização será dada por $$x(t) = x_0 + r cost\;\;\;\;y(t) = y_0 + r \sin{t} \;\;\;\;\;t \in [0, 2 \pi ].$$
A Derivada de Funções Vetoriais
Uma função vetorial f: A \in \mathbb{R} \rightarrow \mathbb{R}^2é derivável em um ponto t_0se cada uma de suas funções coordenadas for derivável neste ponto. Neste caso, a derivada de uma função f(t)é definida por $$f'(t)=\frac{df}{dt} (t) =\left( \frac{dx}{dt} (t) , \frac{dy}{dt} (t) \right).$$ Geometricamente, f'\left(t_0 \right)representa a direção tangente à curva f(t) no ponto t_0, desde que f'\left(t_0 \right) \neq 0.
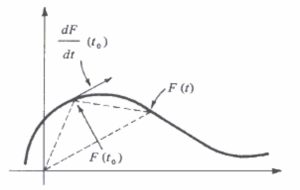Interpretação geométrica da derivada de funções vetoriais no espaço R²
Neste caso, definimos que f'(t_0)é o vetor tangente à trajetória de f, em f(t_0). O que nos leva à equação da reta tangente à curva no ponto f(t_0) no plano: $$\left( x(\lambda), y(\lambda) \right) = f(t_0)+\lambda f'(t_0), \qquad \lambda \in \mathbb{R}.$$
Observações Sobre Matemática Básica Importantes:
- Lembre-se que a geometria plana clássica nos garante que a área do triângulo é dada pela fórmula $$ \text{Área do } \Delta = \frac{\text{Base} \times \text{Altura} }{2};$$
- Um propriedade importante da trigonometria, nos diz que $$ \text{sen}(2 \theta) = 2 \text{sen}(\theta) \text{cos}(\theta).$$
Solução do Exercício
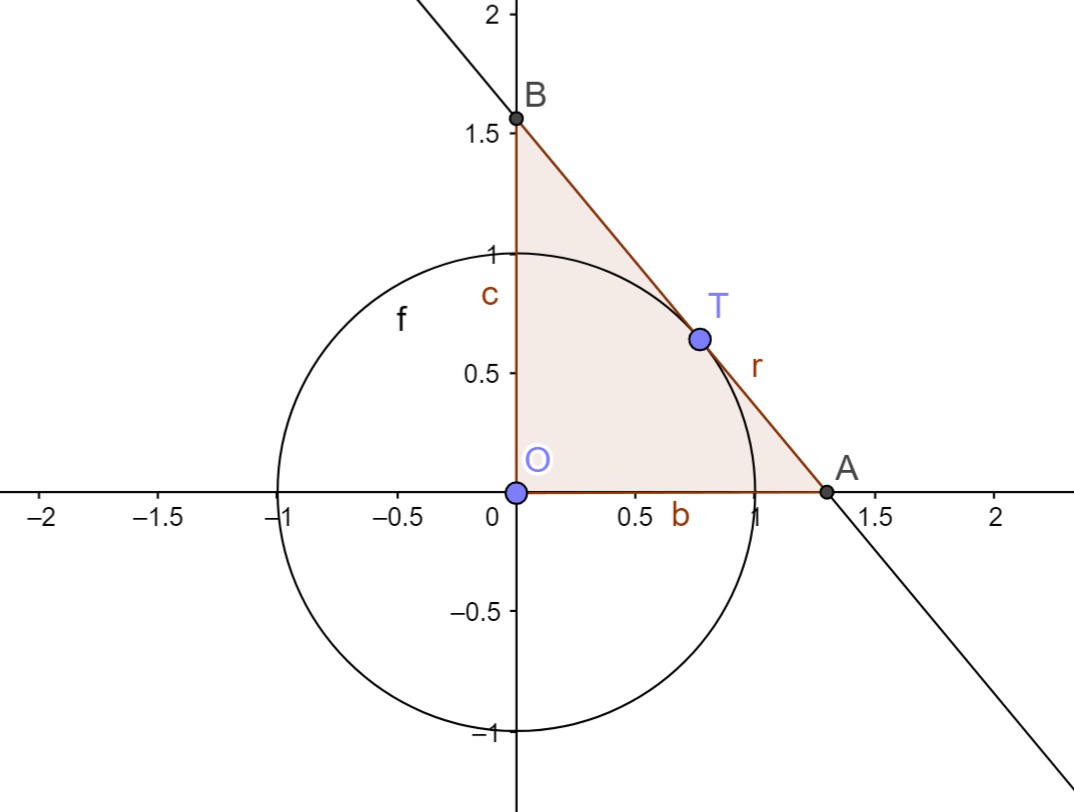
Considere a circunferência descrita pela função vetorial $$\vec{f(t)} = \left( \text{cos}(t), \text{sen}(t) \right), \qquad \text{e} \qquad 0 < \theta < 1.$$ Considere, agora, a reta r tangente a esta circunferência no ponto T = \left( \text{cos}(\theta), \text{sen}(\theta) \right) . Considere O como sendo a origem do plano cartesiano, e A e B os pontos de interseção de r com os eixos coordenados.
Este problema pode ser ilustrado pela figura abaixo:
Suponha, que o ponto A e o ponto B possuam as seguintes coordenadas:
- Como o ponto A está sobre o eixo Ox e sua localização dependerá de qual é o valor de \theta , então suas coordenadas serão $$ A \left( x (\theta ) , 0 \right).$$
- Já o ponto B, como está sobre o eixo Oy, sua localização dependerá de qual é o valor de \theta , então suas coordenadas serão $$ B \left( 0, y (\theta ) \right).$$
Como o triângulo OAB é retângulo em Ô, sabemos que sua área será dada por $$ \text{Área}_{OAB} = \frac{d(O,A) \times d(O,B)}{2 },$$ onde
- d(O,A) = x (\theta ), pois é a distância entre os pontos O e A; e
- d(O,B) = y(\theta ), pois é a distância entre os pontos O e B.
Ou seja, $$ \text{Área}_{OAB} = \frac{ x (\theta ) \times y (\theta ) }{2 }.$$ Agora, para determinar x (\theta ) e y (\theta ) usaremos a equação da reta tangente à circunferência que passa pelo ponto T = \left( \text{cos}(\theta), \text{sen}(\theta) \right) , pois nela estão contidos os dois pontos, A e B.
Para isso, usaremos a equação $$r: \left( x(\lambda), y(\lambda) \right) = \vec{f(t_0)}+\lambda \vec{f'(t_0)}, \qquad \lambda \in \mathbb{R}$$ onde, $$ \vec{f(t_0)} = \left( \text{cos}(\theta), \text{sen}(\theta) \right)$$ e, como, $$ \vec{f(t)} = \left( \text{cos}(t), \text{sen}(t) \right) \Rightarrow \vec{f'(t)} = \left( – \text{sen}(t), \text{cos}(t) \right),$$ então, $$ \vec{f'(t_0)} = \left( -\text{sen}(\theta), \text{cos}(\theta) \right).$$ Donde podemos concluir que a equação vetorial da reta r é dada por $$r: \left( x(\lambda), y(\lambda) \right) = \left( \text{cos}(\theta), \text{sen}(\theta) \right) +\lambda \left( -\text{sen}(\theta), \text{cos}(\theta) \right) , \qquad \lambda \in \mathbb{R}$$ que na forma paramétrica possui equações $$ x(\lambda) = \text{cos} (\theta) – \lambda \text{sen} (\theta) $$ $$ y(\lambda) = \text{sen} (\theta) + \lambda \text{cos} (\theta) $$
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
Agora, observe que:
- Como a coordenada y (\lambda) = 0 no ponto A, então o valor de \lambda para que este ponto seja dado na reta r é $$ y( \lambda ) = 0 \Rightarrow \text{sen} (\theta) + \lambda \text{cos} (\theta) = 0 \Rightarrow $$ $$ \Rightarrow \text{sen} (\theta) = – \lambda \text{cos} (\theta) \Rightarrow \lambda = – \frac{ \text{sen} (\theta)}{ \text{cos} (\theta)}.$$ Ou seja, a coordenada x ( \theta ) no ponto A é dada por $$ x \left( – \frac{ \text{sen} (\theta)}{ \text{cos} (\theta)} \right) = \text{cos} (\theta) + \frac{ \text{sen} (\theta)}{ \text{cos} (\theta)} \text{sen} (\theta) = \frac{\text{cos} ^2 (\theta) + \text{sen} ^2 (\theta)}{\text{cos} (\theta)} = \frac{1}{\text{cos} (\theta)}.$$
- Por outro lado, como a coordenada x ( \lambda ) = 0 no ponto B, então o valor de \lambda para que este ponto seja dado na reta r é, por um raciocínio análogo ao anterior: $$ x ( \lambda ) = 0 \Rightarrow \text{cos} (\theta) – \lambda \text{sen} (\theta) = 0 \Rightarrow \lambda = \frac{ \text{cos} (\theta)}{ \text{sen} (\theta)},$$ o que nos levará à coordenada y ( \theta ) no ponto B dada por $$ y ( \theta ) = \text{sen} (\theta) + \frac{ \text{cos} (\theta)}{ \text{sen} (\theta)} \text{cos} (\theta) = \frac{1}{ \text{sen} (\theta)}.$$
Agora, voltando à área do triângul OAB: $$ \text{Área}_{OAB} = \frac{ x (\theta ) \times y (\theta ) }{2 } = \frac{ \frac{1}{ \text{cos} (\theta)} \times \frac{1}{ \text{sen} (\theta)} }{2 } = \frac{1}{2 \text{cos} (\theta) \text{sen} (\theta) }.$$ Que pela propriedade trigonométrica do seno do arco duplo nos leva a $$ \text{Área}_{OAB} = \frac{1}{2 \text{cos} (\theta) \text{sen} (\theta) } = \frac{1}{\text{sen} (2 \theta) },$$ como queríamos mostrar.
Conclusão:
E assim, chegamos ao final dessa jornada pela geometria do plano. Ao explorar curvas, tangentes e áreas, vimos como conceitos abstratos ganham vida em problemas práticos.
Esse exercício não só reforça as bases do Cálculo 2, mas também revela a beleza sutil das funções vetoriais e suas aplicações. Continue praticando, pois cada desafio resolvido é um passo a mais na compreensão profunda da matemática. A aventura não termina aqui; novos desafios te aguardam!
Precisa de ajuda para resolver exercícios de Cálculo ou Equações Diferenciais? Estamos aqui para facilitar sua jornada matemática! Clique aqui e solicite um orçamento agora mesmo e descubra como podemos te guiar para o sucesso nas disciplinas mais desafiadoras.
